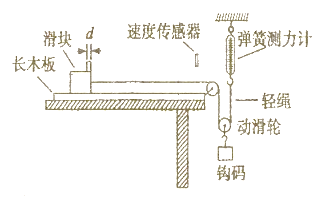
题目内容
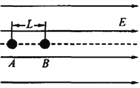
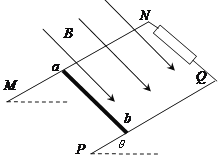
【题目】如图，两条平行的光滑金属轨道MN、PQ与水平面成θ角固定，轨距为d。P、M间接有阻值为R的电阻。质量为m的金属杆ab水平放置在轨道上，其有效阻值为R。空间存在磁感应强度为B的匀强磁场，磁场方向垂直于轨道平面向上。现从静止释放ab。若轨道足够长且电阻不计，重力加速度为g。求：
（1）ab运动的最大速度vm；
（2）当ab具有最大速度时，ab消耗的电功率P；
（3）为使ab向下做匀加速直线运动，在ab中点施加一个平行于轨道且垂直于ab的力F， 推导F随时间t变化的关系式，并分析F的变化与a的关系。
【答案】（1）
；（2）
；（3）
a.当a＜gsinθ时，F方向先沿斜面向上，大小由mgsinθ-ma开始减小到零，随后F方向沿斜面向下，大小从零开始增大。
b. 当a=gsinθ时，F方向沿斜面向下，大小从零开始增大；
c．当a＞gsinθ时，F方向沿斜面向下，大小从ma-mgsinθ开始增大。
【解析】（1）ab具有最大速度时，处于平衡状态，受力分析如图；
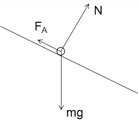
由平衡条件： mgsinθ=FA
FA=BId
由闭合电路欧姆定律： 
得： 
（2）由电功率公式：P=I2R
得： 
（3）ab做匀加速直线运动时，设F沿斜面向下，受力分析如图：
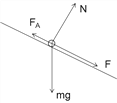
由牛顿运动定律： F+mgsinθ-FA=ma
FA=BId
V=at
得： 
可见：F的大小随时间t呈线性变化
a.当a＜gsinθ时，F方向先沿斜面向上，大小由mgsinθ-ma开始减小到零，随后F方向沿斜面向下，大小从零开始增大。
b. 当a=gsinθ时，F方向沿斜面向下，大小从零开始增大；
c．当a＞gsinθ时，F方向沿斜面向下，大小从ma-mgsinθ开始增大
练习册系列答案
相关题目
