题目内容
据报道，一儿童玩耍时不慎从H=45m高的阳台上无初速掉下，在他刚掉下时恰被楼下一管理员发现，该管理员迅速由静止冲向儿童下落处的正下方楼底，准备接住儿童．已知管理员到楼底的距离为18m，为确保安全能稳妥接住儿童，管理员将尽力节约时间，但又必须保证接儿童时没有水平方向的冲击，不计空气阻力，将儿童和管理员都看做质点，设管理员奔跑过程中只做匀速或匀变速运动，g取10m/s2．问：
（1）管理员至少用多大的平均速度跑到楼底？
（2）若管理员在加速或减速的加速度大小相等，且最大速度不超过9m/s，求管理员奔跑时加速度需满足什么条件？
（1）6m/s (2)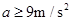 
解析试题分析：（1）设儿童下落时间为t，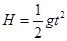
，t =3s
他要能接住儿童，奔跑的时间要小于3s
由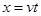
，管理员的平均速度至少为：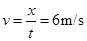
（2）设管理员的加速度为a
由于要求没有水平方向的冲击则
时间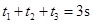
位移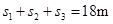
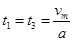
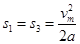
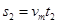
由上可得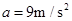
则加速度应满足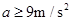
考点：匀变速直线运动规律
点评：本题的主要关系是儿童下落的时间和管理员营救的时间相等，按照此关系应用匀变速直线运动规律分析求解。
练习册系列答案
相关题目