题目内容
(2009?闵行区一模)据报道,一儿童玩耍时不慎从36米高的阳台上无初速掉下,在他刚掉下时恰被楼下社区管理人员发现,该人员迅速由静止冲向儿童下落处的正下方楼底,准备接住儿童.已知管理人员到楼底的距离为18米,为确保能稳妥安全接住儿童,管理人员将尽力节约时间,但又必须保证接儿童时没有水平方向的冲击(即水平速度为零).设儿童下落过程中所受空气阻力约为儿童本身重力的0.2倍,将儿童和管理人员都看作质点,g取10m/s2.
(1)管理人员至少用多大的平均速度跑到楼底?
(2)若管理人员在奔跑过程中做匀加速或匀减速运动的加速度大小相等,且最大速度不超过9m/s,求管理人员奔跑时加速度的大小需满足什么条件?
(1)管理人员至少用多大的平均速度跑到楼底?
(2)若管理人员在奔跑过程中做匀加速或匀减速运动的加速度大小相等,且最大速度不超过9m/s,求管理人员奔跑时加速度的大小需满足什么条件?
分析:(1)儿童掉下做自由落体运动,可以通过自由落体的位移公式求出时间,根据时间再求管理员的最小平均速度.
(2)管理员先加速到速度最大,再匀速,再减速到0,抓住三段时间和等于自由落体的时间,三段位移和等于管理员到楼底的距离,求出最小加速度.
(2)管理员先加速到速度最大,再匀速,再减速到0,抓住三段时间和等于自由落体的时间,三段位移和等于管理员到楼底的距离,求出最小加速度.
解答:解:(1)儿童下落过程作匀加速运动,下落时间为t,加速度为a.
由牛顿第二定律得:mg-0.2mg=ma解得:a=8m/s2
由运动学公式S=
at2得t=
=
=3(s)
管理人员至少用的平均速度为
=
=
=6m/s
(2)设管理人员先匀加速后匀减速奔跑到楼底,奔跑过程中的最大速度为vm,
由运动学公式
=
解得:vm=2
=12m/s
说明管理人员先加速到vm再匀速,最后匀减速奔跑到楼底.设匀速时间为t2,
所以有:S1=
(t2+t)vm t2=
-t=
-3=1(s)
由管理人员奔跑时的加速度为:a=
=
=9m/s2
故管理员加速度要满足a>9m/s2
答:(1)管理人员至少以6m/s平均速度跑到楼底
(2)管理人员奔跑时加速度的大小需满足a>9m/s2.
由牛顿第二定律得:mg-0.2mg=ma解得:a=8m/s2
由运动学公式S=
| 1 |
| 2 |
|
|
管理人员至少用的平均速度为
. |
| v |
| S1 |
| t |
| 18 |
| 3 |
(2)设管理人员先匀加速后匀减速奔跑到楼底,奔跑过程中的最大速度为vm,
由运动学公式
. |
| v |
| 0+vm |
| 2 |
. |
| v |
说明管理人员先加速到vm再匀速,最后匀减速奔跑到楼底.设匀速时间为t2,
所以有:S1=
| 1 |
| 2 |
| 2S1 |
| vm |
| 2×18 |
| 9 |
由管理人员奔跑时的加速度为:a=
| vm |
| t-2t2 |
| 9 |
| 3-2 |
故管理员加速度要满足a>9m/s2
答:(1)管理人员至少以6m/s平均速度跑到楼底
(2)管理人员奔跑时加速度的大小需满足a>9m/s2.
点评:解决本题的关键抓住小孩自由下落的时间和管理员运动的时间相等,灵活运用运动学公式求解.

练习册系列答案
相关题目
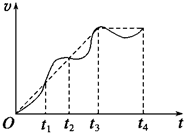 (2009?闵行区一模)某人骑自行车在平直道路上行进,如图中的实线记录了自行车开始一段时间内的v-t图象,某同学为了简化计算,用虚线作近似处理,下列说法正确的是( )
(2009?闵行区一模)某人骑自行车在平直道路上行进,如图中的实线记录了自行车开始一段时间内的v-t图象,某同学为了简化计算,用虚线作近似处理,下列说法正确的是( )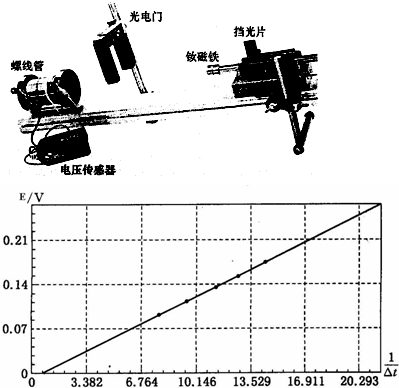 (2009?闵行区一模)在“探索影响感应电动势大小的有关因素实验”中,装置如图所示:
(2009?闵行区一模)在“探索影响感应电动势大小的有关因素实验”中,装置如图所示: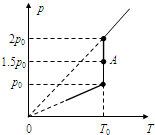 (2009?闵行区一模)某同学利用DIS实验系统研究一定质量的理想气体的状态变化,在实验后计算机屏幕显示了如下的p---T图象(实线部分),已知在A状态气体体积为V0.试求实验过程中,当气体温度保持T0的情况下,气体体积在什么范围内变化?
(2009?闵行区一模)某同学利用DIS实验系统研究一定质量的理想气体的状态变化,在实验后计算机屏幕显示了如下的p---T图象(实线部分),已知在A状态气体体积为V0.试求实验过程中,当气体温度保持T0的情况下,气体体积在什么范围内变化?