题目内容
已知轮船在静水中的速度为v1（保持不变），水流的速度为v2，河宽为d．为使轮船以最短的时间渡河，则v1的方向应该
．为使轮船渡河的位移等于河宽d，必须有v1＞v2，且v1的方向与上游河岸的夹角θ应满足cosθ=
，这样渡河的时间t2=
．
垂直于河岸
垂直于河岸
，渡河的最短时间tmin=| d |
| v1 |
| d |
| v1 |
| v2 |
| v1 |
| v2 |
| v1 |
| d | ||
|
| d | ||
|
分析：船航行时速度为静水中的速度与河水流速二者合速度，当以静水中的速度垂直河岸过河的时候渡河时间最短．由矢量合成的平行四边形定则得知小船的合速度，小船实际以合速度做匀速直线运动，进而求得位移的大小；小船以最短距离过河时，则静水中的速度斜着向上游，合速度垂直河岸．
解答：解：当以静水中的速度垂直河岸过河的时候渡河时间最短，则知：tmin=
小船以最短距离过河时，则静水中的速度斜着向上游，合速度垂直河岸，设与河岸的夹角为θ，
则由矢量合成的平行四边形法则解三角形得：cosθ=
那么船垂直河岸行驶的速度为v=
所以渡河时间t=
故答案为：垂直于河岸；
；
；
．
| d |
| v1 |
小船以最短距离过河时，则静水中的速度斜着向上游，合速度垂直河岸，设与河岸的夹角为θ，
则由矢量合成的平行四边形法则解三角形得：cosθ=
| v2 |
| v1 |
那么船垂直河岸行驶的速度为v=
| v12-v22 |
所以渡河时间t=
| d | ||
|
故答案为：垂直于河岸；
| d |
| v1 |
| v2 |
| v1 |
| d | ||
|
点评：小船过河问题属于运动的合成问题，要明确分运动的等时性、独立性，运用分解的思想，看过河时间只分析垂直河岸的速度，分析过河位移时，要分析合速度．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
一条宽度为d=16m的河流，水流速度为v水=5m/s，已知船在静水中的速度为v船=4m/s，小船从A码头出发，下列说法正确的是（ ）
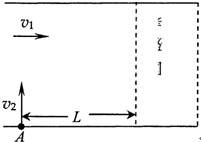如图所示，宽度为200m的河，河水的流速为v1=3m/s，河的下游有一养殖区．已知小船在静水中的速度为v2=4m/s，现让小船从A处驶到对岸且能避开养殖区，小船行驶过程中船头一直垂直指向对岸，则下列说法正确的是（ ）| A、A处与养殖区的距离L至少为120m | B、A处与养殖区的距离L至少为150m | C、船在河中运动的实际速度为5m/s | D、船在河中运动的实际速度为7m/s |