题目内容
8．
图所示，两轮的半径分别为2R和R，两轮通过皮带相连，转动中皮带与轮之间没有打滑现象，A、B分别为两轮子边缘上一点，则A、B两点线速度大小比为1：1，角速度之比为1：2．C点到圆心距离为该轮半径的$\frac{1}{2}$，则B、C两点向心加速度之比为4：1．
分析 靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点具有相同的角速度；根据v=rω，a=ω2r可得出A、B、C三点的角速度之比和向心加速度之比．
解答 解：靠传送带传动轮子边缘上的点具有相同的线速度，故A、B两点的线速度相等，即：vA：vB=1：1；
A的半径是B的半径的2倍，根据v=rω，
知ωA：ωB=1：2．
点A、C共轴转动，角速度相等，即ωA：ωC=1：1．所以ωA：ωB：ωC=1：2：1
B、C具有相同的半径，根据a=rω2，知aB：aC=4：1
故答案为：1：1，1：2，4：1．
点评 解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点具有相同的角速度．掌握线速度与角速度的关系，以及线速度、角速度与向心加速度的关系．
练习册系列答案
相关题目
如图所示（俯视），MN和PQ是两根固定在同一水平面上的足够长且电阻不计的平行金属导轨．两导轨间距为L=0.2m，其间有一个方向垂直水平面竖直向下的匀强磁场B1=5.0T．导轨上NQ之间接一电阻R1=0.40Ω，阻值为R2=$\frac{1}{\sqrt{200}}$Ω的金属杆垂直导轨放置并与导轨始终保持良好接触．两导轨右端通过金属导线分别与电容器C的两极相连．电容器C紧靠着带小孔a（只能容一个粒子通过）的固定绝缘弹性圆筒．圆筒内壁光滑，筒内有垂直水平面竖直向下的匀强磁场B2，O是圆筒的圆心，圆筒的内半径为r=0.40m．
19．关于，下列说法中正确的是（ ）
| A． | 作用力越大，对物体做的功越多 | |
| B． | 在力的方向上物体通过的距离越长，对物体做的功越多 | |
| C． | 小球在光滑水平面上匀速移动10米，没有力对小球做功 | |
| D． | 用10N的力踢足球后，足球在水平面上滚动了20m，踢足球的力做功200J |
如图甲所示，质量m=1kg的物块在平行斜面向上的拉力F作用下从进行开始沿斜面向下运动，t=0.5s时撤去拉力，利用速度传感器得到其速度随时间变化关系图象（v-t图象）如图乙所示，g取10m/s2．求：
3．某同学对着墙壁练习打网球，假定球在墙面以25m/s的速度沿水平方向反弹，落地点到墙面的距离在10m至15m之间，忽略空气阻力，g取10m/s2，则球在墙面上反弹点的高度范围是（ ）
| A． | 0.8～1.8m | B． | 0.8～1.6m | C． | 1.0～1.6m | D． | 1.0～1.8m |
20．
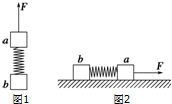a、b两物体的质量分别为m1、m2，由轻质弹簧相连（如图1）．当用恒力F竖直向上拉着a，使a、b一起向上做匀加速直线运动时，弹簧伸长量为x1；当用大小仍为F的恒力沿水平方向拉着a，使a、b一起沿光滑水平桌面做匀加速直线运动时，弹簧伸长量为x2，如图2所示，则（ ）
a、b两物体的质量分别为m1、m2，由轻质弹簧相连（如图1）．当用恒力F竖直向上拉着a，使a、b一起向上做匀加速直线运动时，弹簧伸长量为x1；当用大小仍为F的恒力沿水平方向拉着a，使a、b一起沿光滑水平桌面做匀加速直线运动时，弹簧伸长量为x2，如图2所示，则（ ）| A． | x1一定小于x2 | B． | x1一定等于x2 | C． | 若m1＞m2，则x1＞x2 | D． | 若m1＜m2，则x1＜x2 |
17．如图所示为同一实验室中甲、乙两个单摆的振动图象，从图象可知（ ）
| A． | 两摆球质量相等 | |
| B． | 两单摆的摆长相等 | |
| C． | 两单摆相位相差$\frac{π}{2}$， | |
| D． | 在相同的时间内，两摆球通过的路程总有s甲=2s乙 |
18．下列说法正确的是（ ）
| A． | 光纤通信是光的色散现象的应用 | |
| B． | 紫外线常用于医院和食品消毒，是因为它具有显著的热效应 | |
| C． | 救护车向静止着的你驶来时，你听到的警笛音调变调高，这是声波的多普勒效应 | |
| D． | 照相机镜头的增透膜可以改善相机的透光性能在，这是利用了光的全反射原理 |