题目内容
7.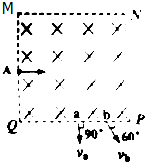 如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场,两个电子(重力不计)分别从MQ之间的某处A沿平行QP方向垂直射入匀强磁场,并分别以不同的速度从a,b射出磁场,射出后与QP夹角分别为90°和60°,求:
如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场,两个电子(重力不计)分别从MQ之间的某处A沿平行QP方向垂直射入匀强磁场,并分别以不同的速度从a,b射出磁场,射出后与QP夹角分别为90°和60°,求:(1)两电子的圆周半径之比ra:rb;
(2)两电子从a,b射出磁场时的速度之比va:vb;
(3)两电子通过匀强磁场所需时间之比ta:tb.
分析 (1)电子在磁场中做匀速圆周运动,作出电子的运动轨迹,由几何知识求出电子的轨道半径,然后求出轨道半径之比.
(2)洛伦兹力提供向心力,应用牛顿第二定律求出电子的速度,然后求出电子的速度之比.
(3)根据电子转过的圆心角与电子做圆周运动的周期公式求出电子运动时间之比.
解答 解:(1)电子运动轨迹如图所示,设AQ=L,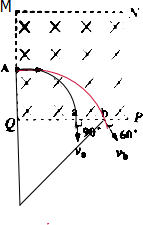
由几何知识得:ra=L,
rb-L=rbsin30°,rb=2L,
轨道半径之比:ra:rb=1:2;
(2)电子做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m$\frac{{v}^{2}}{r}$,解得:v=$\frac{eBr}{m}$∝r,
电子的速度之比:$\frac{{v}_{a}}{{v}_{b}}$=$\frac{{r}_{a}}{{r}_{b}}$=$\frac{1}{2}$;
(3)电子在磁场中做匀速圆周运动的周期:T=$\frac{2πm}{eB}$,
电子在磁场中的运动时间:t=$\frac{θ}{2π}$T=$\frac{θm}{eB}$∝θ,
电子的运动时间之比:$\frac{{t}_{a}}{{t}_{b}}$=$\frac{{θ}_{a}}{{θ}_{b}}$=$\frac{90°}{60°}$=$\frac{3}{2}$;
答:(1)两电子的圆周半径之比ra:rb为1:2;
(2)两电子从a,b射出磁场时的速度之比va:vb为1:2;
(3)两电子通过匀强磁场所需时间之比ta:tb为3:2.
点评 本题考查了电子在磁场中的运动,分析清楚电子的运动过程、作出电子的运动轨迹是解题的关键,应用牛顿定律与电子做圆周运动的周期公式可以解题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
15.甲、乙两车在同一地点同时做直线运动,其x-t图象如图所示,则( )
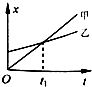

| A. | 两车均做匀加速直线运动 | |
| B. | 两车在t1时刻的速度相等 | |
| C. | 甲车的速度大于乙车的速度 | |
| D. | 0~t1时间内,甲的位移小于乙的位移 |
2.关于电磁波,下列说法中正确的是( )
| A. | 首先预言电磁波存在的物理学家是赫兹 | |
| B. | 麦克斯韦通过实验证实了电磁波的存在 | |
| C. | 电磁波不能在真空中传播 | |
| D. | 在空气中频率越大的电磁波,其波长越小 |
19.下面给出的物理量中,哪些物理量是矢量( )
| A. | 位移 | B. | 力 | C. | 路程 | D. | 加速度 |
17.物体从静止开始做匀加速直线运动,前2s内通过的位移是4m,则( )
| A. | 第1s内的位移是1 m | B. | 第3s末的速度是6 m/s | ||
| C. | 前4s内的平均速度是2 m/s | D. | 第2s内的平均速度是3 m/s |
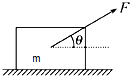 如图所示,在水平面上质量为1kg的物体受一个斜上的拉力F作用,这个力与水平方向成θ=30°,且F=4N,在此力作用下,物体水平向右匀速滑动,求:
如图所示,在水平面上质量为1kg的物体受一个斜上的拉力F作用,这个力与水平方向成θ=30°,且F=4N,在此力作用下,物体水平向右匀速滑动,求: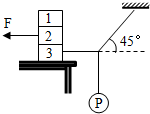 如图所示,三个物块重均为100N,小球P重20N,与3连接的绳子水平,作用在物块2的水平力F=20N,整个系统平衡,则物块3受5个力作用,1和2之间的摩擦力是0N,2和3之间的摩擦力是20N.3与桌面间摩擦力为0N.
如图所示,三个物块重均为100N,小球P重20N,与3连接的绳子水平,作用在物块2的水平力F=20N,整个系统平衡,则物块3受5个力作用,1和2之间的摩擦力是0N,2和3之间的摩擦力是20N.3与桌面间摩擦力为0N.