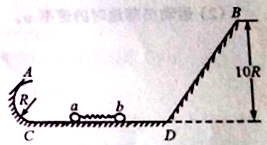
[题目]如图所示.在半径为R 的光滑半圆轨道于高为10R 的光滑斜轨道处于同一竖直平面内.两轨道之间用光滑轨道CD 相连.水平轨道与斜轨道间有一段圆弧过渡.在水平轨道上轻弹簧被A.B 两小球挤压(不栓接)处于静止状态.现同时释放两小球.A 恰好能通过最高点A,B恰好能到达B 点.已知A 的质量为 mA,B 的质量为mB ,求:(1)A 球离开弹簧时的速度vA 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，在半径为R 的光滑半圆轨道于高为10R 的光滑斜轨道处于同一竖直平面内，两轨道之间用光滑轨道CD 相连，水平轨道与斜轨道间有一段圆弧过渡。在水平轨道上轻弹簧被A、B 两小球挤压（不栓接）处于静止状态，现同时释放两小球，A 恰好能通过最高点A；B恰好能到达B 点。已知A 的质量为 mA；B 的质量为mB ；求：

（1）A 球离开弹簧时的速度vA

（2）B 球离开弹簧时的速度 vB

（3）弹簧的弹性势能Ep

【答案】（1）（2）（3）2．5mAgR+10mBgR

【解析】

试题分析：（1）A球过恰好通过圆轨道最高点A时，有：

则得：

A球从C运动到A，由机械能守恒定律得：mAvC2=mAvA2+2mAgR

由以上两式求出：

（2）B球从D运动到B，由机械能守恒定律得：mBvD2=mBg×10R

求得：

（3）弹簧的弹性势能为：Ep=mAvA2+mBvB2

解得：Eρ=2．5mAgR+10mBgR

练习册系列答案

A. m1、m2做圆周运动的角速度之比为2∶3

B. m1、m2做圆周运动的线速度之比为2∶3

C. m1做圆周运动的半径为L

D. m2做圆周运动的半径为L

【题目】如图所示为位于月球背面的我国“嫦娥四号”探测器A通过“鹊桥”中继星B向地球传输电磁波信息的示意图。拉格朗日L2点位于地月连线延长线上，“鹊桥”在L2点附近与月球以相同的周期一起绕地球做匀速圆周运动的同时，还在与地月连线垂直的平面内绕L2点做匀速圆周运动。下列说法正确的是（）

A.“嫦娥四号”的发射速度必须达到第二宇宙速度才能到达月球背面

B.“鹊桥”B绕点做匀速圆周运动的向心力等于地球和月球对它的引力之和

C.“鹊桥”B绕点做匀速圆周运动的半径越大，其相对于点的线速度越小

D.因为月球的自转周期与其绕地球的公转周期相同，所以我们只能看到月球的同一面

【题目】如图所示，在水平圆盘上放有质量分别为m、m、2m的可视为质点的三个物体A、B、C, 圆盘可绕垂直圆盘的中心轴转动.三个物体与圆盘的动摩擦因数均为 ,最大静摩擦力等于滑动摩擦力.三个物体与轴O共线且OA=OB=BC=r=0.2m，现将三个物体用轻质细线相连，保持细线伸直且恰无张力.若圆盘从静止开始转动，且角速度ω缓慢增大，已知重力加速度为g=10m/s2,则对于这个过程，下列说法正确的是

A. A、B两个物体同时达到最大静摩擦力

B. B、C两个物体的静摩擦力先增大后不变

C. 当rad/s时A、B、C整体会发生滑动

D. 当时，在ω增大的过程中B、C间细线的拉力不断增大

【题目】如图所示为一定质量的理想气体的P-V图象，理想气体经历从A→B→C→D→A的变化过程，其中D→A为等温线。已知理想气体在状态B时温度为TB=1000K，在C→D过程中放出热量Q=400J，求

(i)理想气体在状态D时的温度TD；

(ii)C→D过程中理想气体的内能变化量。

【题目】如图所示，小明用与水平方向θ角的轻绳拉木箱，绳中张力为F，沿水平地面向右移动了一段距离l。已知木箱与地面间的动摩擦因数为μ，木箱质量为m，木箱受到的

A. 支持力做功为

B. 重力做功为

C. 拉力做功为

D. 滑动摩擦力做功为

【题目】某学习小组做“探究恒力做功与动能变化的关系”实验如图甲所示。

(1)实验中所用电磁打点计时器是一种使用____（填“交流”或“直流”）电源的计时仪器，它的工作电压是，当电源的频率为50Hz时，它每隔_____s打一次点；

(2)实验中，为了把重物所受的重力作为小车所受的牵引力，需要满足的条件是：

①在未挂重物时，通过垫木块使木板适当倾斜，目的是________________；

②已知小车质量为M，重物质量为m，则M_______ m（填“>”“”“=”“<”或“”）；

(3)选出一条纸带如图乙所示，其中O点为打点计时器打下的第一个点，A、B、C为相邻的三个计数点。用刻度尺测得，，，已知相邻两计数点间时间间隔为T，重力加速度为g则打下B点时小车的速度大小为_______，与之对应小车所受的牵引力做________。

【题目】图中a、b是两个点电荷，它们的电量分别为Q1、Q2，MN是ab连线的中垂线，P是中垂线上的一点，下列哪种情况能使P点场强方向指向MN的左侧( )

A. Q1、Q2都是正电荷，且Q1＞Q2

B. Q1是正电荷，Q2是负电荷，且Q1＞∣Q2∣

C. Q1是负电荷，Q2是正电荷，且∣Q1∣＞Q2

D. Q1、Q2都是负电荷，且∣Q1∣＞∣Q2∣

【题目】某实验小组利用如图甲所示装置测定当地重力加速度的数值。实验开始时，小钢球被电磁铁吸引静止不动，光电门位于钢球的下方，二者的中心处在同一竖直线上。将此时钢球球心位置记为A点，光电门中心位置记为O点，AO间距离为 h。

（1）使用螺旋测微器测定小钢球的直径如图乙所示，可知钢球直径大小为d＝_____mm；

（2）断开电磁铁开关，小钢球由静止开始下落，下落过程中通过位于O点处光电门，由数字计时器记录钢球通过光电门的时间可由表达式v＝_____得到小钢球球心通过光电门时的瞬时速度；

（3）将光电门向下移动一小段距离后，重新釋放小钢球，记录小钢球通过光电门时数字计时器显示的时间△t1和此时光电门与O点间距离x1；重复上述步骤，得到若干组△t和x的数值；在﹣x坐标中描点连线，得到如图丙所示直线并计算出其斜率大小为1.6×105，根据此斜率值，可以得到当地重力加速度的数值为_____m/s2。

试题分类