题目内容
14. 某同学利用如图的装置对轻质弹簧的弹性势能进行探究,将轻质弹簧放置在光滑水平桌面上,左端固定,右端与一小球A接触而不固连,弹簧的原长小于桌面的长度.向左推小球,使弹簧压缩后由静止释放,小球离开桌面后落到水平地面.已知桌面的高度为h,小球质量为m,重力加速度的大小为g,当弹簧的压缩量为△x时,小球抛出点到落地点的水平距离为s,则:
某同学利用如图的装置对轻质弹簧的弹性势能进行探究,将轻质弹簧放置在光滑水平桌面上,左端固定,右端与一小球A接触而不固连,弹簧的原长小于桌面的长度.向左推小球,使弹簧压缩后由静止释放,小球离开桌面后落到水平地面.已知桌面的高度为h,小球质量为m,重力加速度的大小为g,当弹簧的压缩量为△x时,小球抛出点到落地点的水平距离为s,则:(1)小球离开桌面时的速度v=$\sqrt{\frac{g{s}^{2}}{2h}}$(用g,h,s表示);
(2)弹簧压缩△x时的弹性势能E=$\frac{mg{s}^{2}}{4h}$(用g,h,s表示);
(3)若在桌面的边缘放置质量为$\frac{1}{2}$m的另一小球B,重做该实验,保持弹簧的形变量为△x不变,两小球碰撞后落到地面上,小球A落地点与抛出点的水平距离为$\frac{s}{2}$,则小球B落地点与抛出点的水平距离为s.
分析 (1)依据平抛运动规律,结合运动学公式,即可求解;
(2)依据能量守恒定律,结合平抛运动的初速度,即可求解;
(3)根据动量守恒定律,结合竖直方向时间相等,即可求解小球B落地点与抛出点的水平距离.
解答 解:(1)小球离开桌面后,做平抛运动,
因竖直方向做自由落体运动,水平方向做匀速直线运动,
依据平抛运动处理规律,则有:v=$\frac{s}{t}$=$\frac{s}{\sqrt{\frac{2h}{g}}}$=$\sqrt{\frac{g{s}^{2}}{2h}}$,
(2)根据能量守恒定律,弹簧压缩△x时的弹性势能E=$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}×m×(\sqrt{\frac{g{s}^{2}}{2h}})^{2}$=$\frac{mg{s}^{2}}{4h}$;
(3)当弹簧的压缩量为△x时,小球抛出点到落地点的水平距离为s,若在桌面的边缘放置质量为$\frac{1}{2}$m的另一小球B,
保持弹簧的形变量为△x不变,小球A落地点与抛出点的水平距离为$\frac{s}{2}$,
由于竖直方向做自由落体运动,则运动的时间相等,
根据动量守恒定律,则有:mv=mvA+$\frac{m}{2}$vB;
而s=vt,$\frac{s}{2}$=vAt,
那么解得:s′=vBt=s
故答案为:(1)$\sqrt{\frac{g{s}^{2}}{2h}}$;(2)$\frac{mg{s}^{2}}{4h}$;(3)s.
点评 考查平抛运动处理规律,掌握能量守恒定律的内容,理解动量守恒定律的条件及其应用,注意不论是A球,还是B球,在平抛运动时时间是相等,是解题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 某交流电的电压u随时间t变化的曲线为如图所示的正弦曲线,则以下说法正确的是( )
某交流电的电压u随时间t变化的曲线为如图所示的正弦曲线,则以下说法正确的是( )
 某交流电的电压u随时间t变化的曲线为如图所示的正弦曲线,则以下说法正确的是( )
某交流电的电压u随时间t变化的曲线为如图所示的正弦曲线,则以下说法正确的是( )| A. | 该交流电的周期为2s | |
| B. | 该交流电压瞬时值表达式为u=200sin(100πt)V | |
| C. | 用交流电压表测该交流电的电压,示数为200V | |
| D. | 该交流电接在匝数比为20:22的变压器原线圈两端,可以使副线圈中额定电压为220V的电熨斗正常工作 |
5.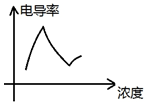 在科学研究中,经常用“电导率”这一概念来表示物质导电本领的强弱,电导率是电阻率的倒数,如图是硫酸浓度与电导率的关系图,下列判断正确的是( )
在科学研究中,经常用“电导率”这一概念来表示物质导电本领的强弱,电导率是电阻率的倒数,如图是硫酸浓度与电导率的关系图,下列判断正确的是( )
 在科学研究中,经常用“电导率”这一概念来表示物质导电本领的强弱,电导率是电阻率的倒数,如图是硫酸浓度与电导率的关系图,下列判断正确的是( )
在科学研究中,经常用“电导率”这一概念来表示物质导电本领的强弱,电导率是电阻率的倒数,如图是硫酸浓度与电导率的关系图,下列判断正确的是( )| A. | 浓度越高导电性能不一定越好 | |
| B. | 可以根据导电率来确定硫酸浓度 | |
| C. | 硫酸的导电性能与其浓度有关,所以对于某一浓度的硫酸导电时,不再遵守欧姆定律 | |
| D. | 浓度确定的硫酸导电时,仍然遵守欧姆定律 |
5.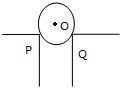 如图所示,一个厚度、材料均匀的薄球壳置于支点P、Q上,支点P、Q等高.在球壳的圆心O正上方有一个小孔,通过小孔向球壳内缓慢地注水,在注水(仍未满)的过程中( )
如图所示,一个厚度、材料均匀的薄球壳置于支点P、Q上,支点P、Q等高.在球壳的圆心O正上方有一个小孔,通过小孔向球壳内缓慢地注水,在注水(仍未满)的过程中( )
 如图所示,一个厚度、材料均匀的薄球壳置于支点P、Q上,支点P、Q等高.在球壳的圆心O正上方有一个小孔,通过小孔向球壳内缓慢地注水,在注水(仍未满)的过程中( )
如图所示,一个厚度、材料均匀的薄球壳置于支点P、Q上,支点P、Q等高.在球壳的圆心O正上方有一个小孔,通过小孔向球壳内缓慢地注水,在注水(仍未满)的过程中( )| A. | 球壳受到支点P的支持力方向不变 | |
| B. | 球壳受到支点P、Q的支持力的夹角越来越小 | |
| C. | 球壳受到的支持力合力不变 | |
| D. | 球壳受到支点P的支持力逐渐增大 |
10.关于热现象,下列说法正确的是( )
| A. | 物体吸收热量,内能一定增加 | |
| B. | 物体吸收热量,内能一定减少 | |
| C. | 温度升高,物体内分子的平均动能一定增加 | |
| D. | 温度升高,物体内每个分子的动能都增加 |

 如图所示,为某同学测定电源电动势E和内阻r的实验电路,图中E为待测电器,A1、A2,V1、V2均为非理想电表,内阻未知,G为灵敏电流计,R1、R2为滑动变阻器,S为开关,实验的主要步骤为:
如图所示,为某同学测定电源电动势E和内阻r的实验电路,图中E为待测电器,A1、A2,V1、V2均为非理想电表,内阻未知,G为灵敏电流计,R1、R2为滑动变阻器,S为开关,实验的主要步骤为: 如图,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径.若在a点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,则圆的半径为$\frac{4(7-4\sqrt{3}){v}_{0}^{2}}{g}$.
如图,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径.若在a点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,则圆的半径为$\frac{4(7-4\sqrt{3}){v}_{0}^{2}}{g}$.