Question

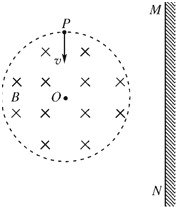
【题目】如图所示，在真空室中平面直角坐标系的y轴竖直向上，x轴上的P点与Q点关于坐标原点O对称，PQ间的距离d=30cm。坐标系所在空间存在一个垂直于xOy平面的圆形有界匀强磁场，一带电粒子在xOy平面内，从P点与x轴成30°的夹角射出，该粒子将做匀速直线运动，已知带电粒子以速度v=2.0m/s射出，质量m=10×10-27kg，所带电荷量q=1.0×10-19C，使带电粒子通过Q点，且其运动轨迹关于y轴对称。已知磁场的磁感应强度大小为B=2.0×10-7T。(不计带电粒子重力)求：

（1）油滴在磁场中运动的时间t；

（2）圆形磁场区域的最小面积S。

Answer 1

【答案】(1) (2)

【解析】带电粒子进入匀强磁场，其轨迹如图所示，

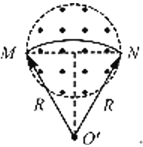
设其做匀速圆周运动设圆周运动的半径为R、运动周期为T、粒子在磁场中运动的时间为t，根据牛顿第二定律：

解得：

所以

设带电粒子从M点进入磁场，从N点射出磁场，由于粒子的运动轨迹关于y轴对称，如图所示，根据几何关系可知∠MO'N=60°，

所以，带电油滴在磁场中运动的时间

(3)连接MN，当MN为圆形磁场的直径时，圆形磁场面积最小，如图所示．根据几何关系圆形磁场的半径r=Rsin30°=0.05m

其面积为：S=πr2=0.0025πm2=7.9×10-3m2．