题目内容
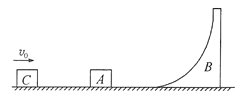
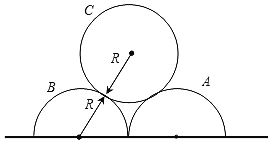
【题目】如图所示，两个半圆柱A、B紧靠着静置于水平地面上，其上有一光滑圆柱C，三者半径均为R，A、B、C的质量都为m，A、B与地面的动摩擦因数均为
。现用水平向右的力拉A,使A缓慢移动,B保持静止,直至C刚要降到地面时,B恰好要发生滑动。设最大静摩擦力等于滑动摩擦力,重力加速度为g，求:
(1)未拉A时,C对B压力的大小；
(2)B与地面的动摩擦因数.
【答案】(1) 
(2) 
【解析】
根据平衡条件和牛顿第三定律求出C对B压力的大小，利用动摩擦公式f=μFN求出动摩擦因数；
解：（1)C受力平衡2Fsin60°=mg
解得F=mg
由牛顿第三定律得C对B的压力大小为F'=F=mg
（2）C恰好降落到地面时，B对C支持力为F2
2 F2sin30°=mg
得F2=mg
C对B压力为F2′= F2=mg
对B有FN= F2′sin30°+mg
f= F2′cos30°
又f=μFN
解得μmin=
练习册系列答案
优百分课时互动系列答案
相关题目
