题目内容
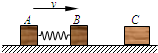 (2007?南京一模)如右图所示,用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑水平地面上运动,弹簧处于原长,质量4kg的物块C静止在前方,B与C碰撞后二者粘在一起运动.在以后的运动中,求:
(2007?南京一模)如右图所示,用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑水平地面上运动,弹簧处于原长,质量4kg的物块C静止在前方,B与C碰撞后二者粘在一起运动.在以后的运动中,求:(1)当弹簧的弹性势能最大时,物体A的速度多大?
(2)弹性势能的最大值是多大?
(3)A的速度有可能向左吗?为什么?
分析:(1)当A、B、C三者的速度相等时弹簧的弹性势能最大,根据A、B、C三者组成的系统动量守恒求解物体A的速度.
(2)分过程研究:BC碰撞过程,由动量守恒求出碰后两者的共同速度.当A、B、C三者的速度相等时弹簧的弹性势能最大,由系统的机械能守恒求出最大的弹性势能.
(3)设A的速度能向左,根据系统的动量守恒,得到B的速度范围,分析三个物体的总动能与系统总机械能的关系,判断A的速度向左是否可能.
(2)分过程研究:BC碰撞过程,由动量守恒求出碰后两者的共同速度.当A、B、C三者的速度相等时弹簧的弹性势能最大,由系统的机械能守恒求出最大的弹性势能.
(3)设A的速度能向左,根据系统的动量守恒,得到B的速度范围,分析三个物体的总动能与系统总机械能的关系,判断A的速度向左是否可能.
解答:解:(1)当A、B、C三者的速度相等时弹簧的弹性势能最大.
由于A、B、C三者组成的系统动量守恒:
(mA+mB)v=(mA+mB+mC)vA′…①
由①式解得 vA′=3m/s…②
(2)B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为v′,则:
mBv=(mB+mC)v′…③
由③式解得:v′=2m/s…④
设物A速度为vA′时,弹簧的弹性势能最大为Ep,根据能量守恒:
Ep=
(mB+mC)v'2+
mAv2-
(mA+mB+mC)
…⑤
由⑤式解得:Ep═12J…⑥
(3)系统动量守恒:mAv+mBv=mAvA+(mB+mC)vB…⑦
设A的速度向左,vA<0,vB>4 m/s
则作用后A、B、C动能之和:
E′=
mAvA2+
(mB+mC)vB2>
(mB+mC)vB2=48 (J)…⑧
实际上系统的总机械能为:
E=Ep+
(mA+mB+mC)
=12+36=48 (J)…⑨
根据能量守恒定律,E'>E是不可能的,所以A不可能向左运动.
答:(1)当弹簧的弹性势能最大时,物体A的速度是3m/s.
(2)弹性势能的最大值是12J.
(3)A的速度不可能向左.
由于A、B、C三者组成的系统动量守恒:
(mA+mB)v=(mA+mB+mC)vA′…①
由①式解得 vA′=3m/s…②
(2)B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为v′,则:
mBv=(mB+mC)v′…③
由③式解得:v′=2m/s…④
设物A速度为vA′时,弹簧的弹性势能最大为Ep,根据能量守恒:
Ep=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
由⑤式解得:Ep═12J…⑥
(3)系统动量守恒:mAv+mBv=mAvA+(mB+mC)vB…⑦
设A的速度向左,vA<0,vB>4 m/s
则作用后A、B、C动能之和:
E′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
实际上系统的总机械能为:
E=Ep+
| 1 |
| 2 |
| v | 2 A |
根据能量守恒定律,E'>E是不可能的,所以A不可能向左运动.
答:(1)当弹簧的弹性势能最大时,物体A的速度是3m/s.
(2)弹性势能的最大值是12J.
(3)A的速度不可能向左.
点评:对于是含有弹簧的系统,抓住系统的合外力为零,遵守两大守恒:动量守恒和机械能守恒进行研究.

练习册系列答案
相关题目
 (2007?南京一模)图中为一“滤速器”装置示意图.a、b为水平放置的平行金属板,一束具有各种不同速率的电子沿水平方向经小孔O进入a、b两板之间.为了选取具有某种特定速率的电子,可在a、b间加上电压,并沿垂直于纸面的方向加一匀强磁场,使所选电子仍能够沿水平直线OO'运动,由O'射出.不计重力作用.可能达到上述目的办法是( )
(2007?南京一模)图中为一“滤速器”装置示意图.a、b为水平放置的平行金属板,一束具有各种不同速率的电子沿水平方向经小孔O进入a、b两板之间.为了选取具有某种特定速率的电子,可在a、b间加上电压,并沿垂直于纸面的方向加一匀强磁场,使所选电子仍能够沿水平直线OO'运动,由O'射出.不计重力作用.可能达到上述目的办法是( ) (2007?南京一模)如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω;电阻R1=10Ω,R2=10Ω,R3=30Ω,R4=35Ω;电容器的电容C=10μF.电容器原来不带电.求接通电键K并达到稳定这一过程中流过R4的总电量.
(2007?南京一模)如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω;电阻R1=10Ω,R2=10Ω,R3=30Ω,R4=35Ω;电容器的电容C=10μF.电容器原来不带电.求接通电键K并达到稳定这一过程中流过R4的总电量. (2007?南京一模)在光滑绝缘的水平台面上,存在平行于水平面向右的匀强电场,电场强度为E.水平台面上放置两个静止的小球A和B(均可看作质点),两小球质量均为m,A球带电荷量为+Q,B球不带电,A、B连线与电场线平行.开始时两球相距L,在电场力作用下,A球开始运动(此时为计时零点,即t=0),后与B球发生对心碰撞,碰撞过程中A、B两球总动能无损失.设在各次碰撞过程中,A、B两球间无电量转移,且不考虑两球碰撞时间及两球间的万有引力.
(2007?南京一模)在光滑绝缘的水平台面上,存在平行于水平面向右的匀强电场,电场强度为E.水平台面上放置两个静止的小球A和B(均可看作质点),两小球质量均为m,A球带电荷量为+Q,B球不带电,A、B连线与电场线平行.开始时两球相距L,在电场力作用下,A球开始运动(此时为计时零点,即t=0),后与B球发生对心碰撞,碰撞过程中A、B两球总动能无损失.设在各次碰撞过程中,A、B两球间无电量转移,且不考虑两球碰撞时间及两球间的万有引力.
 (2007?南京一模)在如图所示的水平导轨(摩擦、电阻忽略不计)处于竖直向下的匀强磁场中,磁场的磁感强度B,导轨左端的间距为L1=4l0,右端间距为L2=4l0,两段导轨均足够长.今在导轨上放置AC、DE两根导体棒,质量分别为m1=2m0,m2=m0.电阻分别为R1=4R0,R2=R0.若AC棒以初速度v0向右运动,求:
(2007?南京一模)在如图所示的水平导轨(摩擦、电阻忽略不计)处于竖直向下的匀强磁场中,磁场的磁感强度B,导轨左端的间距为L1=4l0,右端间距为L2=4l0,两段导轨均足够长.今在导轨上放置AC、DE两根导体棒,质量分别为m1=2m0,m2=m0.电阻分别为R1=4R0,R2=R0.若AC棒以初速度v0向右运动,求: