题目内容
19. 如图,一矩形导线框ABCD处于水平匀强磁场中绕垂直于磁场的轴OO′匀速转动,线圈的面积是0.5m2,线圈电阻为r=1Ω,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$T,线框输出端通过电刷与电流表、理想变压器原线圈相连,副线圈两端接有一只“18V、12W”的灯泡L.当线框转速n=50r/s时,灯泡L正常发光,此时电流表示数为0.2A.
如图,一矩形导线框ABCD处于水平匀强磁场中绕垂直于磁场的轴OO′匀速转动,线圈的面积是0.5m2,线圈电阻为r=1Ω,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$T,线框输出端通过电刷与电流表、理想变压器原线圈相连,副线圈两端接有一只“18V、12W”的灯泡L.当线框转速n=50r/s时,灯泡L正常发光,此时电流表示数为0.2A.(1)求通过灯泡L的电流周期
(2)求变压器原、副线圈匝数之比
(3)从线框ABCD图中所示位置开始计时,写出线框中产生的感应电流瞬时值的表达式
(4)若由(线圈平面与磁感线平行)位置转过30°角,则此过程中产生的平均感应电动势多大.
分析 明确变压器原理,知道变压器不会改变周期,根据电压之比等于匝数之比可求得匝数之比;
根据有效值和最大值之间的关系可求得电流最大值,则可求得表达式;
根据法拉第电磁感应定律可求得平均值.
解答 解:(1)变压器不改变交变电流的周期,故通过灯泡的电流周期等于线框转动的周期,故T=0.02s;
(2)设原经圈两端的电压为U1,根据功率公式可得:
P1=I1U1
解得:U1=60V;
根据变压比公式可得,
$\frac{{U}_{1}}{{U}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$
解得:$\frac{{n}_{1}}{{n}_{2}}$=$\frac{10}{3}$;
(3)线框转动的角速度ω=2πn=2π×50=100πrad/s;
线框中感应电流的最大值Im=0.2$\sqrt{2}$A;
线框中感应电流的瞬时值i=Imsinωt=0.2$\sqrt{2}$sin100πtA;
(4)在线圈与磁场平行位置时磁通量为0;
在转了30°时磁通量Φ2=BSsin30°=$\frac{2}{π}$×$0.5×\frac{1}{2}$=$\frac{\sqrt{2}}{4π}$A;
转30°所用的时间△t=$\frac{\frac{π}{6}}{100π}$=$\frac{1}{600}$s;
则平均电动势E=$\frac{△Φ}{△t}$=$\frac{\frac{\sqrt{2}}{4π}}{\frac{1}{600}}$=$\frac{150\sqrt{2}}{π}$V;°
答:(1)通过灯泡L的电流周期为0.02s;
(2)变压器原、副线圈匝数之比为10:3;
(3)从线框ABCD图中所示位置开始计时,写出线框中产生的感应电流瞬时值的表达式i=0.2$\sqrt{2}$sin100πtA
(4)若由(线圈平面与磁感线平行)位置转过30°角,则此过程中产生的平均感应电动势为$\frac{150\sqrt{2}}{π}$V
点评 本题考查交流电的性质及变压器原理,要注意明确变压器电压之比等于线圈匝数之比,并明确有效值、最大值及平均值的计算方法.

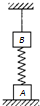 如图所示,轻质弹簧连接A、B两物体,A放在水平地面上,B的上端通过细线悬挂在天花板上;已知A的重力为8N、B的重力为6N、弹簧的弹力为4N.则地面受到的压力大小和细线受到的拉力大小可能是( )
如图所示,轻质弹簧连接A、B两物体,A放在水平地面上,B的上端通过细线悬挂在天花板上;已知A的重力为8N、B的重力为6N、弹簧的弹力为4N.则地面受到的压力大小和细线受到的拉力大小可能是( )| A. | 18 N和10 N | B. | 4 N和10 N | C. | 12 N和2 N | D. | 14 N和2 N |
| A. | 开普勒认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 | |
| B. | 奥斯特发现了电流的周围存在磁场并最早提出了场的概念 | |
| C. | 牛顿认为在足够高的高山上以足够大的水平速度抛出一物体,物体就不会再落在地球上 | |
| D. | 安培首先引入电场线和磁感线,极大地促进了他对电磁现象的研究 |
| A. | 多普勒效应是由波的干涉引起的 | |
| B. | 人们感觉不到次声波,次声波可不知不觉地杀死人 | |
| C. | 交通管理应用了多普勒效应 | |
| D. | 医用B超应用了多普勒效应 |
| A. | 磁场看不见,摸不着,所以不存在 | |
| B. | 磁场是人为假设的 | |
| C. | 磁场只存在于磁铁周围 | |
| D. | 磁极间相互作用,都是通过磁场来实现的 |
 如图,在半径为r的轴上悬挂着一个质量为M的水桶P,轴上均匀分布着6根手柄,每个柄端固定有质量均为m的金属球,球离轴心的距离为l,轮轴、绳和手柄的质量及摩擦均不计.现由静止释放水桶,整个装置开始转动.
如图,在半径为r的轴上悬挂着一个质量为M的水桶P,轴上均匀分布着6根手柄,每个柄端固定有质量均为m的金属球,球离轴心的距离为l,轮轴、绳和手柄的质量及摩擦均不计.现由静止释放水桶,整个装置开始转动.

 墙上固定一个小圆环,一小球用线系住穿过圆环靠于墙上,如图所示,当从圆环到小球之间的细线在变长的过程中,线受到的拉力和球对墙的压力是如何变化的?
墙上固定一个小圆环,一小球用线系住穿过圆环靠于墙上,如图所示,当从圆环到小球之间的细线在变长的过程中,线受到的拉力和球对墙的压力是如何变化的?