题目内容
【题目】如图所示，半圆玻璃砖的半径R=12cm，直径AB与光屏MN垂直并接触于A点。一束激光a从半圆弧表面上射向半圆玻璃砖的圆心O，光线与竖直直径AB之间的夹角为60°，最终在光屏MN上出现两个光斑，且A点左侧光斑与A之间距离为4
cm。求：
①玻璃砖的折射率；
②改变激光a的入射方向，使光屏MN上只剩一个光斑，求此光斑离A点的最远距离。
【答案】（1）
（2）
【解析】
（1）根据折射定律和反射定律作出光路图，根据几何关系求出折射角，从而求得玻璃砖的折射率；
（2）改变入射角，使屏MN上只剩一个光斑，此光斑离A最远时，恰好发生全反射，入射角等于临界角C，由sinC
求得临界角C．再由几何知识求此光斑离A点的最长距离。
（1）由题意可得，激光在AB面上发生折射的入射角
，设半圆玻璃砖的折射率为
，折射角为
，
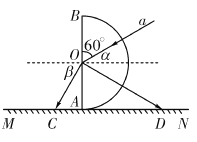
则：
；
其中：
；
解得：
（2）分析可得，当激光在AB面上恰好发生全反射时，光屏MN上只剩一个光斑且光斑离A点的距离最远，
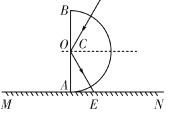
所以：设激光在AB面上恰好发生全反射时的临界角为C，由折射定律可得：
光斑离A点的距离最远：
由数学知识可得：
代入数据可得：
练习册系列答案
相关题目
