题目内容
如图所示，两条平行的金属导轨相距L=lm，水平部分处在竖直向下的匀强磁场B1中，倾斜部分与水平方向的夹角为37°，处于垂直于斜面的匀强磁场B2中，两部分磁场的大小均为0.5T。 金属棒MN和PQ的质量均为m=0.2kg，电阻分别为RMN=0.5Ω和RPQ=1.5Ω。MN置于水平导轨上，与水平导轨间的动摩擦因数μ=0.5，PQ置于光滑的倾斜导轨上，两根金属棒均与导轨垂直且接触良好。从t=0时刻起，MN棒在水平外力F1的作用下由静止开始以a=2m/s2的加速度向右做匀加速直线运动，PQ则在平行于斜面方向的力F2作用下保持静止状态。不计导轨的电阻，水平导轨足够长，MN始终在水平导轨上运动。求：
（1）t=5s时，PQ消耗的电功率；
（2）t=0～2.0s时间内通过PQ棒的电荷量；
（3）规定图示F1、F2方向作为力的正方向，分别求出F1、F2随时间t变化的函数关系；
（4）若改变F1的作用规律，使MN棒的运动速度v与位移s满足关系：
，PQ棒仍然静止在倾斜轨道上。求MN棒从静止开始到s=5m的过程中，F1所做的功。
解答与评分标准：
（1）金属棒MN在t=5s时的速度 
电动势
（1分）
电流 
（1分）
（1分）
（2）t=0～2.0s时间内金属棒MN运动的位移
（1分）
t=0～2.0s时间内穿过回路MNQP磁通量的变化量
（1分）
t=0～2.0s时间内通过PQ棒的电荷量
（1分）
（3）金属棒MN做匀加速直线运动过程中，
对MN运用牛顿第二定律得：
（1分）
代入数据得：
（1分）
金属棒PQ处于静止状态，根据平衡条件得：
（1分）
代入数据得：
（1分）
（4）MN棒做变加速直线运动，当s=5m时，
因为速度v与位移s成正比，所以电流I、安培力也与位移s成正比，
安培力做功WB=-
（2分）
MN棒动能定理： 
（1分）
（1分）
阅读快车系列答案
如图所示，两条平行的长直金属细导轨KL、PQ固定于同一水平面内，它们之间的距离为l，电阻可忽略不计；ab和cd是两根质量皆为m的金属细杆，杆与导轨垂直，且与导轨良好接触，并可沿导轨无摩擦地滑动．两杆的电阻皆为R．杆cd的中点系一轻绳，绳的另一端绕过轻的定滑轮悬挂一质量为M的物体，滑轮与转轴之间的摩擦不计，滑轮与杆cd之间的轻绳处于水平伸直状态并与导轨平行．导轨和金属细杆都处于匀强磁场中，磁场方向垂直于导轨所在平面向上，磁感应强度的大小为B．现两杆及悬物都从静止开始运动，当ab杆及cd杆的速度分别达到v1和v2时，两杆加速度的大小各为多少？
如图所示，两条平行的金属导轨MP、NQ与水平面夹角为α，设导轨足够长．导轨处在与导轨平面垂直的匀强磁场中，磁感应强度B=0.80T，与导轨上端相连的电源电动势E=4.5V，内阻r=0.4Ω，水平放置的导体棒ab的电阻R=1.5Ω，两端始终与导轨接触良好，且能沿导轨无摩擦滑动，与导轨下端相连的电阻R1=1.0Ω，电路中其它电阻不计．当单刀双掷开关S与1接通时，导体棒刚好保持静止状态，求：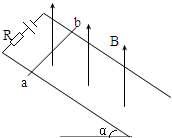
如图所示，两条平行的足够长的光滑金属导轨与水平面成α=53°角，导轨间距离L=0.8m．其上端接一电源和一固定电阻，电源的电动势E=1.5V，其内阻及导轨的电阻可忽略不计．固定电阻R=4.5Ω．导体棒ab与导轨垂直且水平，其质量m=3×10-2kg，电阻不计．整个装置处于竖直向上的匀强磁场中，磁感应强度B=0.5T．（g=10m/s2 sin53°=0.8 cos53°=0.6 ）
（2008?福州模拟）如图所示，两条平行的足够长的光滑金属导轨与水平面成α=37°角，导轨间距离L=0.6m，其上端接一电容和一固定电阻，电容C=10μF，固定电阻R=4.5Ω．导体棒ab与导轨垂直且水平，其质量m=3×10-2kg，电阻r=0.5Ω．整个装置处于垂直导轨平面向上的匀强磁场中，已知磁感应强度B=0.5T，取g=10m/s2，sin37°=0.8，cos37°=0.6．现将ab棒由静止释放，当它下滑的速度达到稳定时，求：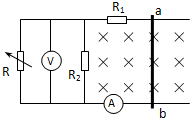
如图所示，两条平行的光滑水平导轨上，用套环连着一质量为0.2kg、电阻为2Ω的导体杆ab，导轨间匀强磁场的方向垂直纸面向里．已知R1=3Ω，R2=6Ω，电压表的量程为0～10V，电流表的量程为0～3A（导轨的电阻不计）．求：