题目内容
10.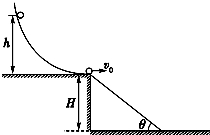 光滑曲面轨道置于高度为H=1.8m的平台上,其末端切线水平;另有一长木板两端分别搁在轨道末端点和水平地面间,构成倾角为θ=37°的斜面,如图所示.一个可视作质点的质量为m=1kg的小球,从光滑曲面上由静止开始下滑(不计空气阻力,g取10m/s2,sin37°≈0.6,cos37°≈0.8)
光滑曲面轨道置于高度为H=1.8m的平台上,其末端切线水平;另有一长木板两端分别搁在轨道末端点和水平地面间,构成倾角为θ=37°的斜面,如图所示.一个可视作质点的质量为m=1kg的小球,从光滑曲面上由静止开始下滑(不计空气阻力,g取10m/s2,sin37°≈0.6,cos37°≈0.8)(1)若小球从高h=0.2m处下滑,则小球离开平台时速度v0的大小是多少?
(2)若小球下滑后正好落在木板的末端,则释放小球的高度h为多大?
分析 (1)小球下滑过程中受重力和支持力,其中支持力不做功,只有重力做功,机械能守恒,根据机械能守恒定律列式求解v0;
(2)先根据平抛运动的位移公式求解出平抛的初速度,然后对沿斜面下滑过程运用机械能守恒定律列式求解h.
解答 解:(1)小球从曲面上滑下,只有重力做功,由机械能守恒定律知:
mgh=$\frac{1}{2}$mv2 ①
得v0=$\sqrt{2gh}$=$\sqrt{2×10×0.2}$m/s=2m/s
(2)小球离开平台后做平抛运动,小球正好落在木板的末端,则
H=$\frac{1}{2}$gt2 ②
$\frac{H}{tanθ}$=v1t ③
联立②③两式得:v1=4m/s
设释放小球的高度为h1,则由 mgh1=$\frac{1}{2}$mv2
得h1=0.8m
答:
(1)若小球从高h=0.2m处下滑,则小球离开平台时速度v0的大小是2m/s.
(2)若小球下滑后正好落在木板的末端,则释放小球的高度h是0.8m.
点评 本题关键是将平抛运动沿着水平和竖直方向正交分解,根据位移时间关系公式和速度时间关系列式联立求解.

练习册系列答案
相关题目
11.物体在几个恒力的共同作用下做匀速直线运动,若突然撤去其中一个力,物体不可能做的运动形式是( )
| A. | 匀速直线运动 | B. | 匀加速直线运动 | C. | 匀减速直线运动 | D. | 匀变速曲线运动 |
2.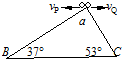 如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
 如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )| A. | 16:9 | B. | 9:16 | C. | 1:1 | D. | 4:3 |
20.在远距离输电时,发电厂输送的电功率一定,只考虑输电线的焦耳热损失,当发电厂把输送电压提升到原来的2倍后,输电效率会从原来的92%变为( )
| A. | 90% | B. | 94% | C. | 96% | D. | 98% |
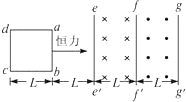 两个沿竖直方向的磁感应强度大小相等、方向相反的匀强磁场穿过光滑的水平桌面,它们的宽度均为L.质量为m、边长为L的平放在桌面上的正方形线圈的ab边与磁场边界ee′平行且两者间的距离为L,如图所示.线圈在恒力作用下由静止开始沿桌面加速运动,ab边进入左边的磁场时恰好做速度为v的匀速直线运动,求:
两个沿竖直方向的磁感应强度大小相等、方向相反的匀强磁场穿过光滑的水平桌面,它们的宽度均为L.质量为m、边长为L的平放在桌面上的正方形线圈的ab边与磁场边界ee′平行且两者间的距离为L,如图所示.线圈在恒力作用下由静止开始沿桌面加速运动,ab边进入左边的磁场时恰好做速度为v的匀速直线运动,求: