题目内容
【题目】如图所示为一装置的截面图,其中AB段是半径为R=2L的四分之一圆轨道,CDO段为半径r=L的半圆形轨道,最高点O固定一个竖直挡板,小球碰后原速弹回,D为CDO轨道的中点,两轨道均光滑,如图连接且固定,现有一个质量为m的小球以某一速度v从A点进入轨道,并在竖直平面的轨道内运动。求:
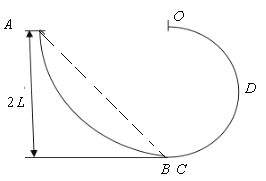
(1)若要小球做完整的圆周运动,从A点进入轨道的速度v至少是多少?
(2)若小球从某一高度静止释放,且轨道承受最大压力为3mg,试分析小球应从轨道上离地面多高的位置释放。
(3)若轨道不光滑,小球以某一速度从A点进入轨道后,经挡板弹回时恰好返回A点,若将圆轨道AB换成直轨道(虚线所示),且与CDO圆弧光滑连接,直轨道的动摩擦因数和圆轨道相同,若小球以相同大小的速度从A点进入直轨道后,能再次返回A点吗,请简述原因。
【答案】(1)![]() (2)L (3)能通过A点且具有一定的速度
(2)L (3)能通过A点且具有一定的速度
【解析】(1)当小球恰好通过O点,由牛顿第二定律知![]() ,因为r=L,得
,因为r=L,得 ![]()
因为A、O等高,所以若要小球做完整的圆周运动,从A点进入轨道的速度v至少为![]()
(2)设经过最低点C的速度为![]() ,则
,则
![]()
![]()
得![]()
若小球在离地面为h的高度静止释放,根据动能定理
![]()
得h=L
故应从离地面高为L的位置静止释放
(3)若换成斜面,斜面的摩擦力做功变小,所以损失的机械能变小,故能通过A点且具有一定的速度。

练习册系列答案
相关题目