题目内容
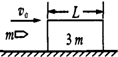
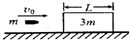
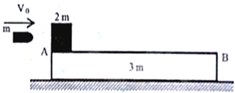 如图所示,质量为3m的木板静止在光滑的水平面上,一个质量为2m的物块(可视为质点),静止在木板上的A端,已知物块与木板间的动摩擦因数为μ.现有一质量为m的子弹(可视为质点)以初速度v0水平向右射入物块并穿出,已知子弹穿出物块时的速度为
如图所示,质量为3m的木板静止在光滑的水平面上,一个质量为2m的物块(可视为质点),静止在木板上的A端,已知物块与木板间的动摩擦因数为μ.现有一质量为m的子弹(可视为质点)以初速度v0水平向右射入物块并穿出,已知子弹穿出物块时的速度为| v0 | 2 |
①子弹穿出物块时物块的速度大小.
②子弹穿出物块后,为了保证物块不从木板的B端滑出,木板的长度至少多大?
分析:①设子弹穿过物块时,对子弹和物块组成的系统,由于所受的外力远小于内力,系统的动量守恒,根据动量守恒定律求解子弹穿出物块时物块的速度大小.
②物块刚好到达木板右端时,板的长度最短,此时物块和木板达到共同的速度,对于它们组成的系统,运用动量守恒定律和能量守恒定律列式,即可求得木板的长度.
②物块刚好到达木板右端时,板的长度最短,此时物块和木板达到共同的速度,对于它们组成的系统,运用动量守恒定律和能量守恒定律列式,即可求得木板的长度.
解答:解:①设子弹穿过物块时物块的速度为v1,对子弹和物块组成的系统,由动量守恒定律得:
mv0=m
+2mv1,
解得,v1=
②物块和木板达到的共同速度为v2时,物块刚好到达木板右端,这样板的长度最小为L,对物块和木板组成的系统,由动量守恒得:
2mv1=5mv2,
此过程系统摩擦生热:Q=2μmgL
由能量守恒定律得:2μmgL=
?2m
-
?5m
代入数据解得:L=
答:①子弹穿出物块时物块的速度大小是
.②子弹穿出物块后,为了保证物块不从木板的B端滑出,木板的长度至少为
.
mv0=m
| v0 |
| 2 |
解得,v1=
| v0 |
| 4 |
②物块和木板达到的共同速度为v2时,物块刚好到达木板右端,这样板的长度最小为L,对物块和木板组成的系统,由动量守恒得:
2mv1=5mv2,
此过程系统摩擦生热:Q=2μmgL
由能量守恒定律得:2μmgL=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
代入数据解得:L=
3
| ||
| 160μg |
答:①子弹穿出物块时物块的速度大小是
| v0 |
| 4 |
3
| ||
| 160μg |
点评:本题综合考查了动量守恒定律和能量守恒定律,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
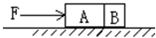 如图所示,质量为3m的光滑物体A与质量为m的光滑物体B,放在水平面上,在水平推力F从左向右的推力作用下加速运动,则A和B的相互作用力大小为
如图所示,质量为3m的光滑物体A与质量为m的光滑物体B,放在水平面上,在水平推力F从左向右的推力作用下加速运动,则A和B的相互作用力大小为 如图所示,质量为3m的物块A和质量为m的物块B与地面的摩擦均不计,在已知水平力F的作用下,A、B一起做匀加速直线运动,则二者的加速度为
如图所示,质量为3m的物块A和质量为m的物块B与地面的摩擦均不计,在已知水平力F的作用下,A、B一起做匀加速直线运动,则二者的加速度为
 (1)通过α粒子散射实验
(1)通过α粒子散射实验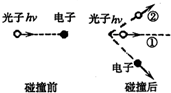 (1)如图所示为康普顿效应示意图,光子与一个静止的电子发生碰撞,图中标出了碰撞后电子的运动方向.设碰前光子频率为v,碰后为v′,则关于光子碰后的运动方向和频率的说法中正确的是
(1)如图所示为康普顿效应示意图,光子与一个静止的电子发生碰撞,图中标出了碰撞后电子的运动方向.设碰前光子频率为v,碰后为v′,则关于光子碰后的运动方向和频率的说法中正确的是