��Ŀ����
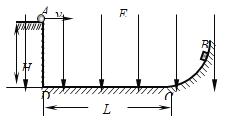
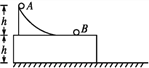
����Ŀ��(16��)��ͼ��ʾ,ˮƽ�����Ϲ̶��и�Ϊh��ƽ̨,̨�����й̶��Ĺ⻬�µ�,�µ����˾�̨���ҲΪh,�µ�����̨������.С��A���µ������ɾ�ֹ��ʼ����,����ˮƽ�⻬��̨����뾲ֹ��̨���ϵ�С��B������ײ,��ճ����һ��,��ͬ��̨�滬�в���̨���Ե�ɳ�,��ص���ɳ����ˮƽ����ǡ��Ϊ̨�ߵ�һ��.���������Ϊ�ʵ�,���Կ�������,�������ٶ�Ϊg.��
(1)С��A�ջ���ˮƽ̨����ٶ�vA;
(2)A��B���������֮��mA��mB.
���𰸡���1��![]() ��2��1:3
��2��1:3
���������⣺��1��С��A�»������У��ɶ��ܶ����ɵã�
mAgh=![]() mAvA2��0����ã�vA=
mAvA2��0����ã�vA=![]() ��
��
��2��A��B������ײʱ�����غ㣬
�ɶ����غ㶨�ɿɵã�mAvA=��mA+mB��v��
�뿪ƽ̨��������ƽ���˶���
ˮƽ����![]() =vt��
=vt��
��ֱ����h=![]() gt2��
gt2��
��ã�mA��mB=1��3��
�𣺣�1��С��A�ջ���ˮƽ̨����ٶ�![]() ��
��
��2��A��B���������֮��ΪmA��mB=1��3��

��ϰ��ϵ�д�
�����Ŀ