题目内容
磁悬浮列车是一种高速运载工具．它具有两个重要系统：一是悬浮系统，利用磁力使车体在导轨上悬浮起来；另一是驱动系统，在沿轨道上安装的三相绕组中，通上三相交流电，产生随时间和空间做周期性变化的磁场，磁场与固连在车体下端的感应金属板相互作用，使车体获得牵引力．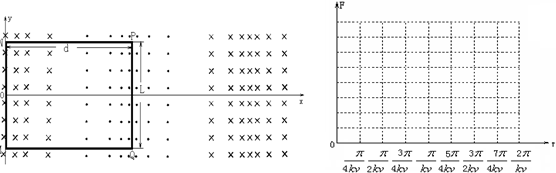
设图中xOy平面代表轨道平面，x轴与轨道平行，现有一与轨道平面垂直的磁场正以速度v向-x方向匀速运动，设在t=0时，该磁场的磁感应强度B的大小随空间位置x的变化规律为B=B0coskx（式中B0、k为已知常量），且在y轴处，该磁场垂直xOy平面指向纸里．与轨道平面平行的一金属矩形框MNPQ处在该磁场中，已知该金属框的MN边与轨道垂直，长度为L，固定在y轴上，MQ边与轨道平行，长度为d=
，金属框的电阻为R，忽略金属框的电感的影响．求：
（1）t=0时刻，金属框中的感应电流大小和方向；
（2）金属框中感应电流瞬时值的表达式；
（3）经过t=
时间，金属框产生的热量；
（4）画出金属框受安培力F随时间变化的图象．
设图中xOy平面代表轨道平面，x轴与轨道平行，现有一与轨道平面垂直的磁场正以速度v向-x方向匀速运动，设在t=0时，该磁场的磁感应强度B的大小随空间位置x的变化规律为B=B0coskx（式中B0、k为已知常量），且在y轴处，该磁场垂直xOy平面指向纸里．与轨道平面平行的一金属矩形框MNPQ处在该磁场中，已知该金属框的MN边与轨道垂直，长度为L，固定在y轴上，MQ边与轨道平行，长度为d=
| π |
| k |
（1）t=0时刻，金属框中的感应电流大小和方向；
（2）金属框中感应电流瞬时值的表达式；
（3）经过t=
| 10π |
| kv |
（4）画出金属框受安培力F随时间变化的图象．
分析：（1）根据切割感应电动势与闭合电路欧姆定律，即可确定感应电流的大小，再由右手定则可确定感应电流的方向；
（2）根据闭合电路欧姆定律，与运动学公式，即可求解；
（3）根据焦耳定律，即可求解；
（4）根据安培力的表达式，结合前面的结论，从而可根据关系式，作出图象．
（2）根据闭合电路欧姆定律，与运动学公式，即可求解；
（3）根据焦耳定律，即可求解；
（4）根据安培力的表达式，结合前面的结论，从而可根据关系式，作出图象．
解答：解：（1）磁场向-x方向运动，等效金属框向x方向运动．
t=0时刻，金属框产生的电动势e=2B0Lv
由闭合电路欧姆定律，则有 i=
=
电流的方向根据右手定则可知为M→N→P→Q→M
（2）设经过时间t，金属框MN所在处磁场强度为B，i=
=
cos(kx)
又x=vt，得到电流瞬时值的表达式是：i=
cos(kvt)，是正弦式电流．
（3）根据焦耳定律，则有Q=(
)2Rt=
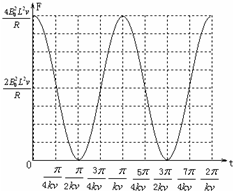
（4）金属框受安培力的方向始终向左．设经过时间t，
金属框受到安培力为F安=2BiL=
=
cos2(kvt)=
[cos(2kvt)+1]
由此可知：金属框受到安培力F随时间变化的图象如右图：
答：（1）t=0时刻，金属框中的感应电流大小
和方向为M→N→P→Q→M；
（2）金属框中感应电流瞬时值的表达式：i=
cos(kvt)；
（3）经过t=
时间，金属框产生的热量
；
（4）画出金属框受安培力F随时间变化的图象如上图所示．
t=0时刻，金属框产生的电动势e=2B0Lv
由闭合电路欧姆定律，则有 i=
| e |
| R |
| 2B0Lv |
| R |
电流的方向根据右手定则可知为M→N→P→Q→M
（2）设经过时间t，金属框MN所在处磁场强度为B，i=
| 2BLv |
| R |
| 2B0Lv |
| R |
又x=vt，得到电流瞬时值的表达式是：i=
| 2B0Lv |
| R |
（3）根据焦耳定律，则有Q=(
| Im | ||
|
20π
| ||
| kR |
（4）金属框受安培力的方向始终向左．设经过时间t，
金属框受到安培力为F安=2BiL=
| 4B2L2v |
| R |
4
| ||
| R |
2
| ||
| R |
由此可知：金属框受到安培力F随时间变化的图象如右图：
答：（1）t=0时刻，金属框中的感应电流大小
| 2B0Lv |
| R |
（2）金属框中感应电流瞬时值的表达式：i=
| 2B0Lv |
| R |
（3）经过t=
| 10π |
| kv |
20π
| ||
| kR |
（4）画出金属框受安培力F随时间变化的图象如上图所示．
点评：考查法拉第电磁感应定律、闭合电路欧姆定律与焦耳定律，掌握右手定则，注意与左手定则的区别，同时由电流的有效值来确定热量的多少，最后掌握安培力的表达式，突出电流变化的关系式．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
磁悬浮列车是一种高速运载工具，它由两个系统组成．一是悬浮系统，利用磁力使车体在轨道上悬浮起来从而减小阻力．另一是驱动系统，即利用磁场与固定在车体下部的感应金属线圈相互作用，使车体获得牵引力，图22就是这种磁悬浮列车电磁驱动装置的原理示意图．即在水平面上有两根很长的平行轨道PQ和MN，轨道间有垂直轨道平面的匀强磁场B1和B2，且B1和B2的方向相反，大小相等，即B1=B2=B．列车底部固定着绕有N匝闭合的矩形金属线圈abcd（列车的车厢在图中未画出），车厢与线圈绝缘．两轨道间距及线圈垂直轨道的ab边长均为L，两磁场的宽度均与线圈的ad边长相同．当两磁场Bl和B2同时沿轨道方向向右运动时，线圈会受到向右的磁场力，带动列车沿导轨运动．已知列车车厢及线圈的总质量为M，整个线圈的总电阻为R．
（2008?天津）磁悬浮列车是一种高速低耗的新型交通工具．它的驱动系统简化为如下模型，固定在列车下端的动力绕组可视为一个矩形纯电阻金属框，电阻为R，金属框置于xOy平面内，长边MN长为l平行于y轴，宽度为d的NP边平行于x轴，如图1所示．列车轨道沿Ox方向，轨道区域内存在垂直于金属框平面的磁场，磁感应强度B沿Ox方向按正弦规律分布，其空间周期为λ，最大值为B0，如图2所示，金属框同一长边上各处的磁感应强度相同，整个磁场以速度v0沿Ox方向匀速平移．设在短暂时间内，MM、PQ边所在位置的磁感应强度随时间的变化可以忽略，并忽略一切阻力．列车在驱动系统作用下沿Ox方向加速行驶，某时刻速度为v（v＜v0）．