Question

【题目】1772年，法籍意大利数学家拉格朗日在论文《三体问题》指出：两个质量相差悬殊的天体（如太阳和地球）所在同一平面上有5个特殊点，如图中的L1、L2、L3、L4、L5所示，人们称为拉格朗日点．若飞行器位于这些点上，会在太阳与地球共同引力作用下，可以几乎不消耗燃料而保持与地球同步绕太阳做圆周运动。北京时间2011年8月25日23时27分， “嫦娥二号”在世界上首次实现从月球轨道出发，受控准确进入距离地球约150万公里远的拉格朗日L2点的环绕轨道。若发射一颗卫星定位于拉格朗日L2点，进行深空探测，下列说法正确的是（ ）

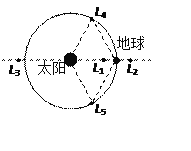
A. 该卫星绕太阳运动的向心加速度小于地球绕太阳运动的向心加速度

B. 该卫星绕太阳运动周期和地球自转周期相等

C. 该卫星在L2处所受太阳和地球引力的合力比在L1处小

D. 该卫星在L1点处于受到地球和太阳的引力的大小相等

Answer 1

【答案】B

【解析】A、据题意知，卫星与地球同步绕太阳做圆周运动，则卫星绕太阳运动周期和地球公转周期相等，公转半径大于地球的公转半径，根据向心加速度，该卫星绕太阳运动的向心加速度大于地球绕太阳运动的向心加速度，故A错误、B正确；

C、由题可知，卫星在L1点与L2点的周期与角速度是相等的，根据向心力的公式：F=mω2r，在L1点处的半径小，所以在L1点处的合力小，C错误；

D、该卫星在L1处所受的合力为地球和太阳对它引力的合力，合力提供向心力，不为零，地球和太阳的引力的大小不相等，D错误。

故选：B。