题目内容
【题目】如图所示是滑梯简化图,一小孩从滑梯上A点开始无初速度下滑,在AB段匀加速下滑,在BC段匀减速下滑,滑到C点恰好静止,整个过程中滑梯保持静止状态。假设小孩在AB段和BC段滑动时的动摩擦因数分别为μ1和μ2,AB与BC长度相等,则( )
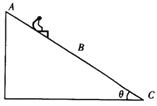
A. 整个过程中地面对滑梯始终无摩擦力作用
B. 动摩擦因数μ1+μ2=2tanθ
C. 小孩从滑梯上A点滑到C点先超重后失重
D. 整个过程中地面对滑梯的支持力先小于小孩和滑梯的总重力后大于小孩和滑梯的总重力
【答案】BD
【解析】小朋友在AB段做匀加速直线运动,将小朋友的加速度a1分解为水平和竖直两个方向,由于小朋友有水平向右的分加速度即有向右的力,根据牛顿定律知,地面对滑梯的摩擦力方向先水平向右;有竖直向下的分加速度,则由牛顿第二定律分析得知:小孩处于失重,地面对滑梯的支持力FN小于小朋友和滑梯的总重力.同理,小朋友在BC段做匀减速直线运动时,小孩处于超重,地面对滑梯的支持力大于小朋友和滑梯的总重力,地面对滑梯的摩擦力方向水平向左.故AC错误,D正确.设AB的长度为L,AB间的高度为h,则sinθ=![]() ,小孩在B点的速度为v.小孩从A到B为研究对象,由动能定理得:-μ1mgLcoosθ+mgh=
,小孩在B点的速度为v.小孩从A到B为研究对象,由动能定理得:-μ1mgLcoosθ+mgh=![]() mv2-0;
mv2-0;
小孩从B到C为研究过程,由动能定理得:-μ2mgLcosθ+mgh=0-![]() mv2;联立并代入数据得:μ1+μ2=2tanθ,故B正确.故选BD.
mv2;联立并代入数据得:μ1+μ2=2tanθ,故B正确.故选BD.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目