题目内容
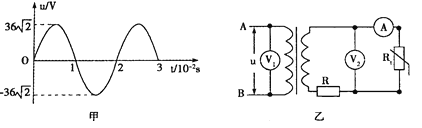
【题目】随着智能手机的使用越来越广泛,一些人在驾车时也常常离不开手机。然而开车使用手机是一种分心驾驶的行为,极易引发交通事故。如图甲所示,一辆出租车在平直公路上以v0=20m/s的速度匀速行驶,此时车的正前方x0=100m处有一电动三轮车,正以v1=8m/s速度匀速行驶,而出租车司机此时正低头看手机,3.5s后才发现危险,司机立刻采取紧急制动措施。若从司机发现危险开始计时,出租车的速度-时间图象如图乙所示,g取10m/s2。
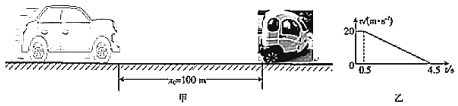
(1)假若出租车与三轮车不发生碰撞,从司机低头看手机到出租车停止运动的这段时间内,出租车前进的距离;
(2)通过计算判断三轮车是否被撞。
【答案】(1)120m(2)三轮车不会被撞
【解析】
(1)从乙图可知司机的反应时间是0.5s,在低头看手机到开始制动这段时间内,出租车做匀速直线运动,出租车前进的距离为: x1=v0t=20×(3.5+0.5)m=80m
刹车后到出租车停止,出租车前进的距离为: x2=![]() ×20×4m=40m
×20×4m=40m
所以从司机低头看手机到出租车停止运动的这段时间内,
出租车前进的距离为: x=x1+x2=120m
(2)出租车减速运动的加速度为: a=![]() =m/s2=-5m/s2
=m/s2=-5m/s2
若出租车减速至三轮车的速度时还没撞上,则之后不会撞上,所以以出租车速度减至v1=8m/s为末状态研究,有:v1=v0+at2
代入数据解得:t2=2.4s
司机从低头看手机到出租车减速为v1=8m/s所前进的位移为:
x出租车=x1+![]() =80m+
=80m+![]() m=113.6m
m=113.6m
这段时间内三轮车前进的距离为: x三轮车=8×(3.5+0.5+2.4)m=51.2m
由于x三轮车+x0=151.2m>x出租车,所以三轮车不会被撞。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目