题目内容
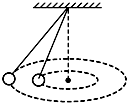如图所示，两个质量不同的小球用长度不等的细线拴在同一点，并在离地面某一高度的同一水平面内做匀速圆周运动，则它们的（ ）| A、周期相同 | B、线速度的大小相等 | C、角速度的大小相等 | D、向心加速度的大小相等 |
分析：两个小球均做匀速圆周运动，对它们受力分析，找出向心力来源，可先求出角速度，再由角速度与线速度、周期、向心加速度的关系公式求解！
解答：解：A、C、对其中一个小球受力分析，如图，受重力，绳子的拉力，由于小球做匀速圆周运动，故合力提供向心力；
将重力与拉力合成，合力指向圆心，由几何关系得，合力：
F=mgtanθ ①
由向心力公式得到：
F=mω2r ②
设绳子与悬挂点间的高度差为h，由几何关系，得：
r=htanθ ③
由①②③三式得：
ω=
，与绳子的长度和转动半径无关，故C正确；
又由T=
=2π
，周期与绳子长度无关，故A正确；
B、由v=ωr，两球转动半径不等，所以线速度不等，故B错误；
D、由a=ω2r，两球转动半径不等，所以向心加速度不等，故D错误；
故选：AC．
将重力与拉力合成，合力指向圆心，由几何关系得，合力：
F=mgtanθ ①
由向心力公式得到：
F=mω2r ②
设绳子与悬挂点间的高度差为h，由几何关系，得：
r=htanθ ③
由①②③三式得：
ω=
|
又由T=
| 2π |
| ω |
|
B、由v=ωr，两球转动半径不等，所以线速度不等，故B错误；
D、由a=ω2r，两球转动半径不等，所以向心加速度不等，故D错误；
故选：AC．
点评：本题关键要对球受力分析，找向心力来源，求角速度；同时要灵活应用角速度与线速度、周期、向心加速度之间的关系公式！
练习册系列答案
相关题目
如图所示，两个质量分别为m1=2kg，m2=3kg的物体置于光滑的水平面上，中间用轻质弹簧秤连接．两个大小分别为F1=30N、F2=20N的水平拉力分别作用在m1、m2上，则（ ）
如图所示，两个质量相等的物体A、B处在同一水平线上，当物体A被水平抛出的同时，物体B开始自由下落，图中曲线AC为物体A的运动轨迹，直线BD为物体B的运动轨迹，两轨迹相交于O点，空气阻力忽略不计，则（ ）
（2010?宿州二模）如图所示，两个质量各为mA和mB的小球A和B，分别系在一条跨过定滑轮的柔软轻绳的两端，不计滑轮轴的摩擦、滑轮的质量和空气阻力，已知mA＞mB，开始时，A、B两球以等大的初速度V0分别竖直向下和竖直向上运动，当A物体下降距离为h时，A、B速度大小都为Vt，试利用牛顿运动定律及匀变速直线运动规律，证明在此运动过程中，A、B组成的系统机械能守恒．
