题目内容
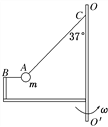
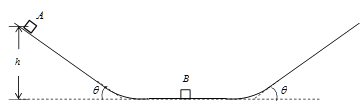
【题目】如图所示,两光滑斜面与光滑水平面间夹角均为![]() ,两斜面末端与水平面平滑对接。可视为质点的物块A、B质量分别为m、βm(β为待定系数),物块A从左边斜面h高处由静止开始沿斜面下滑,与静止于水平轨道的物块B正面相撞,碰后物块A、B立即分开,它们能达到的最大高度均为
,两斜面末端与水平面平滑对接。可视为质点的物块A、B质量分别为m、βm(β为待定系数),物块A从左边斜面h高处由静止开始沿斜面下滑,与静止于水平轨道的物块B正面相撞,碰后物块A、B立即分开,它们能达到的最大高度均为![]() 。两物块经过斜面与水平面连接处及碰撞过程中均没有机械能损失,重力加速度为g。求:
。两物块经过斜面与水平面连接处及碰撞过程中均没有机械能损失,重力加速度为g。求:
(1)待定系数β;
(2)第一次碰撞刚结束时木块A、B各自的速度;
(3)物块A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论木块A、B在轨道最低处第n次碰撞刚结束时各自的速度。
【答案】(1)3;(2)![]() ,方向向左;
,方向向左;![]() ,方向向右;(3)见解析。
,方向向右;(3)见解析。
【解析】
试题分析:(1)由 ![]() ,得
,得 ![]()
(2)设 A、B 碰撞后的速度分别为 v1、v2,
则 ![]()
![]()
设向右为正、向左为负,解得
![]() ,方向向左
,方向向左
![]() ,方向向右
,方向向右
(3)规定向右为正方向,设 A、B 第二次碰撞刚结束时的速度分别为 V1、V2,则
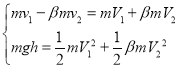
解得![]() (另一组解:V1=-v1,V2=-v2 不合题意,舍去)
(另一组解:V1=-v1,V2=-v2 不合题意,舍去)
由此可得:
当 n为奇数时,小球 A、B 在第 n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同;
当 n为偶数时,小球 A、B 在第 n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同。

练习册系列答案
相关题目