题目内容
如图所示,质量为m的滑块从h高处的a点沿倾斜轨道ab滑入水平轨道bc,滑块与轨道的动摩擦因数处处相同.滑块在a、c两点时的速度大小均为v,ab与bc长度相等.不计空气阻力,忽略在连接处b点的能量损失.则滑块从a到c的运动过程中( )
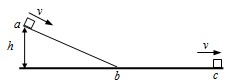
| A.ab、bc两阶段运动时间相等 | ||
| B.ab、bc两阶段加速度大小相等 | ||
C.经b点时的速度大于
| ||
| D.ab、bc两阶段损失的机械能相等 |

A、设物块在b点时的速度为v′,则ab阶段:v′2-v2=2a1s
bc阶段:v2-v′2=-2a2s
可见:a1=a2
又v′-v=at,
则两阶段运动时间也相等;故AB正确;
C、对全程运用动能定理得,mgh-Wf=0,全程克服阻力做功等于mgh,因为ab段所受的支持力小于重力,所以所受的摩擦力小于bc段所受摩擦力,则ab段克服摩擦力做功小于
mgh.
对ab段根据动能定理得:mgh-Wf=
mv′2-
mv2,因为Wf<
mgh,所以v′>
,故C正确;
D、两阶段克服摩擦力做功不相等,故损失的机械能不相等,D错误;
故选:ABC.
bc阶段:v2-v′2=-2a2s
可见:a1=a2
又v′-v=at,
则两阶段运动时间也相等;故AB正确;
C、对全程运用动能定理得,mgh-Wf=0,全程克服阻力做功等于mgh,因为ab段所受的支持力小于重力,所以所受的摩擦力小于bc段所受摩擦力,则ab段克服摩擦力做功小于
| 1 |
| 2 |
对ab段根据动能定理得:mgh-Wf=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v2+gh |
D、两阶段克服摩擦力做功不相等,故损失的机械能不相等,D错误;
故选:ABC.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目