题目内容
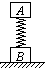
如图所示,水平地面上有一质量为m的物体,其上表面固定一根直立的轻质弹簧,倔强系数为K.现将弹簧上端A缓慢地竖直提起距离h,使物体离开地面,这时物体的重力势能是______(以地面为势能零点),整个过程中拉力做功为______,弹簧的弹性势能为______.
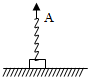

物块刚A离开地面时,弹簧所受的弹力等于物块的重力,根据胡克定律得:
弹簧伸长的长度为:x=
=
由弹簧上端B缓慢的竖直向上提起的距离h,则物块上升的高度为:L=h-x
以地面为势能零点,这时物块A具有的重力势能为:
Ep=mgL=mg(h-x)=mg(h-
)
由于缓慢提起,物体处于平衡状态,拉力F=mg,则拉力做的功为:WF=mgh;
根据动能定理:WF-W弹-mgL=0-0,
得:W弹=mgh-mgL=
则弹簧的弹性势能增加为:EP=
故答案为:mg(h-
);mgh;
.
弹簧伸长的长度为:x=
| F |
| k |
| mg |
| k |
由弹簧上端B缓慢的竖直向上提起的距离h,则物块上升的高度为:L=h-x
以地面为势能零点,这时物块A具有的重力势能为:
Ep=mgL=mg(h-x)=mg(h-
| mg |
| k |
由于缓慢提起,物体处于平衡状态,拉力F=mg,则拉力做的功为:WF=mgh;
根据动能定理:WF-W弹-mgL=0-0,
得:W弹=mgh-mgL=
| m2g2 |
| k |
则弹簧的弹性势能增加为:EP=
| m2g2 |
| k |
故答案为:mg(h-
| mg |
| k |
| m2g2 |
| k |

练习册系列答案
相关题目


 h
h