题目内容
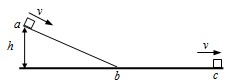
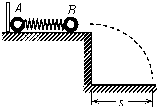
质量相等的A、B两球之间压缩一根轻弹簧,静置于光滑台面上.当用板挡住小球A而只释放B球时,B球被弹出落于桌边距离为s的水平地面上,如图所示.问当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,B球的落地点离桌边为( )
A.
| B.
| C.s | D.
|

当用板挡住A球而只释放B球时,B球做平抛运动.设高度为h,则有vB=s
,所以弹性势能为
E=
m
=
,当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律可得:
0=mvA-mvB所以vA:vB=1:1.因此A球与B球获得的动能之比EkA:EkB=1:1.所以B球的获得动能为:
.
那么B球抛出初速度为vB=
,
则平抛后落地水平位移:x=
×
=
s,
故选:D
|
E=
| 1 |
| 2 |
| v | 2B |
| mgs2 |
| 4h |
0=mvA-mvB所以vA:vB=1:1.因此A球与B球获得的动能之比EkA:EkB=1:1.所以B球的获得动能为:
| mgs2 |
| 8h |
那么B球抛出初速度为vB=
| s |
| 2 |
|
则平抛后落地水平位移:x=
| s |
| 2 |
|
|
| ||
| 2 |
故选:D

练习册系列答案
相关题目
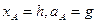 B、
B、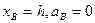
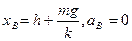 D、
D、