��Ŀ����
����Ŀ����ͼ��ʾ��һ����Ǧ�=30��Ĺ⻬б�涥���ж����֣�����Ϊm��A�������ڵ��沢�ھ���ϵ��Ϊk����ֱ�ᵯ��������һ������������֣�һ����б��������Ϊm��B��������������б��ƽ�У�����һ���뵯���϶����ӣ���ʼʱ����B����ǡ��ֱ���ɴ���ԭ��״̬���ֽ�B�ɾ�ֹ�ͷţ�B�»�������Aǡ�����뿪���浫��������������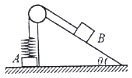
��1��B�»�����͵�ʱ�ļ��ٶȣ�
��2������B���廻������Ϊ3m��C��C��������ʼλ�þ�ֹ�ͷţ���A����պ�Ҫ�뿪����ʱ��C�ٶȵ�ƽ��Ϊ���v2= ��
���𰸡�
��1���⣺��A�����Ҫ�뿪����ʱ��A������������Ϊ0����A���壺��ƽ�������ã�F��mg=0��
�ã�F=mg
��B����ļ��ٶȴ�СΪa����B���壬��ţ�ٵڶ����ɵã�F��mgsin��=ma
��ã�a= ![]() g��B������ٶȵķ�����б�����ϣ�
g��B������ٶȵķ�����б�����ϣ�
��B�»�����͵�ʱ�ļ��ٶ�Ϊ ![]() g��������б�����ϣ�
g��������б�����ϣ�
��2��![]()
���������⣺��2��ԭ�����ɴ���ԭ��״̬����A�����Ҫ�뿪����ʱ��A���崦��ƽ��״̬����C������б���»�x�����쳤��Ϊx��
��A������kx��mg=0
��ã�x= ![]()
A�����Ҫ�뿪����ʱ�����ɵĵ����������ӡ�E����B�����»��Ĺ��̣��������غ㶨���У���E=mgxsin��
��C�����»��Ĺ��̣��������غ㶨���У���E+ ![]() =3mgxsin��
=3mgxsin��
��ã�v2= ![]() ��2��
��2�� ![]() ��
��
�����㾫����������Ĺؼ���������ܹ�ϵ�����֪ʶ�����յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1��