题目内容
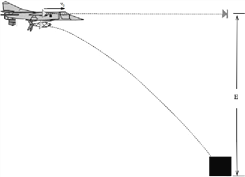
【题目】如图所示，竖直放置的光滑圆环上，穿过一个绝缘小球，小球质量为m，带电量为q，整个装置置于水平向左的匀强电场中.今将小球从与环心O在同一水平线上的A点由静止释放，它沿顺时针方向运动到环的最高点D时速度恰好为零，则：
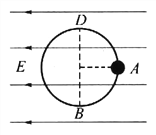
(1)电场强度大小为多大?
(2)小球到达最低点B时对环的压力为多大?
【答案】（1）mg/q （2）5mg
【解析】小球在运动过程中受到重力、电场力与环的弹力作用，环的弹力对小球不做功；
（1）从A到D的过程中，由动能定理得：-mgr+qEr=0-0，
解得：E=
；
（2）从A到B的过程中，由动能定理得：mgr+qEr=
mv2-0
解得：v=2
；
小球在B点做圆周运动，环的支持力与重力的合力提供向心力，由牛顿第二定律得：
F-mg=m
培优三好生系列答案
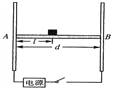
优化作业上海科技文献出版社系列答案【题目】小华同学在做“用打点计时器测速度”的实验时，从打下的若干纸带中选出了如图所示的一条纸带，已知打点计时器使用的电源频率为50 Hz，每两个相邻计数点间有四个点没有画出，各计数点到0点的距离如纸带上所示．
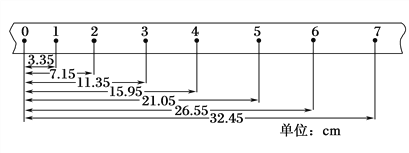
(1)为了达到实验的目的，除了有打点计时器、纸带、小车、细绳、导线、低压交流电源、小木块、长木板外，还需要的仪器有______
A．刻度尺 B．铁架台
C．停表 D．天平
(2)图中两计数点的时间间隔为T＝________s.
(3)根据纸带提供的信息，小华同学已经计算出了打下1、2、3、4、6这五个计数点时小车的速度，请你帮助他计算出打下计数点5时小车的速度v5＝________m/s(结果保留3位有效数字)，并填入表中.
计数点 | 1 | 2 | 3 | 4 | 5 | 6 |
t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
v/(m·s－1) | 0.358 | 0.400 | 0.440 | 0.485 | 0.570 |
(4)以速度v为纵轴、时间t为横轴在坐标纸上建立直角坐标系，根据表中的v、t数据，在坐标系中描点，并作出小车运动的v－t图象．
(5)根据v－t图象可知，小车运动的加速度大小为________ m/s2(结果保留3位有效数字)．
