题目内容
 (2011?海南)(1)一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.关于这列简谐波,下列说法正确的是
(2011?海南)(1)一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.关于这列简谐波,下列说法正确的是CD
CD
(填入正确选项前的字母.选对1个给2分,选对2个给4分;选错1个扣2分,最低得0分).A.周期为4.0s B.振幅为20cm
C.传播方向沿x轴正向 D.传播速度为10m/s

(2)一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端s1=0.8m处有一浮标,示意如图.一潜水员在浮标前方s2=3.0m处下潜到深度为h2=4.0m时,看到标记刚好被浮标挡住,此处看不到船尾端Q;继续下潜△h=4.0m,恰好能看见Q.求
( i)水的折射率n;
( ii)赛艇的长度l.(可用根式表示)
分析:(1)由简谐运动的表达式可知该波的周期,由图象可知该波的振幅、波长;则可求得波速;由带动法可知P点的振动方向;
(2)i由题意可作出光路图,由几何关系可知入射角和折射角,则可求得折射率;
ii由题意可知潜水员和Q点的连线与水平方向夹角刚好为临界角,由几何关系可解得赛艇的长度.
(2)i由题意可作出光路图,由几何关系可知入射角和折射角,则可求得折射率;
ii由题意可知潜水员和Q点的连线与水平方向夹角刚好为临界角,由几何关系可解得赛艇的长度.
解答:解:(1)ω=5π周期为:T=
=0.4s,由波的图象得:振幅A=10cm、波长λ=4m,故波速为v=
=10m/s,p点在t=0时振动方向为正y方向,波向正x方向传播
故答案为CD;
(2)( i)设过P点光线,恰好被浮子挡住时,入射角、折射角分别为:α、β则:sinα=
①、sinβ=
②、n=
③由①②③得:n=
( ii)潜水员和Q点连线与竖直方向的夹角刚好为临界角C,则:sinC=
=
④
由几何知识解得:cotC=
cotC=
⑤
由④⑤得:l=(
-3.8)m

| 2π |
| ω |
| λ |
| T |
故答案为CD;
(2)( i)设过P点光线,恰好被浮子挡住时,入射角、折射角分别为:α、β则:sinα=
| s1 | ||
|
| s2 | ||
|
| sinα |
| sinβ |
| 4 |
| 3 |
( ii)潜水员和Q点连线与竖直方向的夹角刚好为临界角C,则:sinC=
| 1 |
| n |
| 3 |
| 4 |
由几何知识解得:cotC=
| ||
| 3 |
cotC=
| h2+△h |
| s1+s2+l |
由④⑤得:l=(
| 24 |
| 7 |
| 7 |

点评:本题以光的直线传播为基础,利用几何知识,研究光传播到两种介质的界面时发生的反射、折射、全反射、色散等现象和它们表现的规律,即光的反射和折射定律,难点是光的全反射及其应用.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 (2011?海南)一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )
(2011?海南)一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )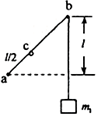 (2011?海南)如图,墙上有两个钉子a和b,它们的连线与水平方向的夹角为45°,两者的高度差为l.一条不可伸长的轻质细绳一端固定于a点,另一端跨过光滑钉子b悬挂一质量为m1的重物.在绳子距a端
(2011?海南)如图,墙上有两个钉子a和b,它们的连线与水平方向的夹角为45°,两者的高度差为l.一条不可伸长的轻质细绳一端固定于a点,另一端跨过光滑钉子b悬挂一质量为m1的重物.在绳子距a端 (2011?海南)如图,水平地面上有一个坑,其竖直截面为半圆.ab为沿水平方向的直径.若在a点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,求圆的半径.
(2011?海南)如图,水平地面上有一个坑,其竖直截面为半圆.ab为沿水平方向的直径.若在a点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,求圆的半径.