题目内容
【题目】如图所示，水平地面上放置一个质量为m的物体，在与水平方向成θ角、斜向右上方拉力的拉力F的作用下沿水平地面运动．物体与地面间的动摩擦因数为μ，重力加速度为g．求：
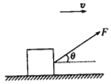
（1）若物体在拉力F的作用下能始终沿水平面向右运动且不脱离地面，拉力F的大小范围．
（2）已知m=10kg，μ=0.5，g=10m/s2，若F的方向可以改变，求物体以恒定加速度a=5m/s2向右做匀加速直线运动时，拉力F的最小值．
【答案】（1）
（2）
【解析】试题分析：要使物体不离开水平面，拉力竖直方向上的分力小于等于重力，物体能向右运动，拉力在水平方向上的分力大于摩擦力，从而得出拉力的大小范围；根据牛顿第二定律求出来啦的表达式，结合数学知识求出拉力最小值的表达式，从而得出拉力的最小值。
（1）要使物体运动时不离开水平面，拉力竖直方向上的分力小于等于重力级：Fsinθ≤mg
要使物体能向右运动，应有拉力在水平方向上的分力大于摩擦力即：Fcosθ≥μ（mg﹣Fsinθ）
联立以上解得： 
（2）根据牛顿第二定律得： 
解得： 
上式变形可得：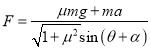 
，其中
当
时，F有最小值，解得： 
，
带入数据解得： 
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
