题目内容
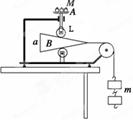
如图,一条长为L 的细线,上端固定,下端拴一质量为m的带电小球。将它置于一电场强度大小为E、方向水平的匀强电场中。已知当细线离开竖直线的偏角为α=30°时,小球处于平衡,问: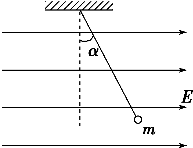
(1)小球带何种电荷?所带电荷量多少?
(2)如果细线的偏角由α增大到θ=60°,然后将小球由静止释放,则在细线摆到竖直位置时,小球的速度为多大?
(1)负电  (2)v=0
(2)v=0
解析试题分析:
(1)根据受力分析图可知,小球带负电。小球在平衡位置时满足: ,解得
,解得 ;
;
(2)设小球摆到最低点时的速度为v,则由动能定理: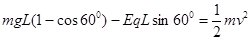 ,解得v=0.
,解得v=0.
考点:力的平衡及动能定理。

练习册系列答案
相关题目
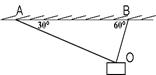
在竖直平面内固定一半径为 的金属细圆环,质量为
的金属细圆环,质量为 的金属小球(视为质点)通过长为
的金属小球(视为质点)通过长为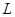 的绝缘细线悬挂在圆环的最高点.当圆环、小球都带有相同的电荷量
的绝缘细线悬挂在圆环的最高点.当圆环、小球都带有相同的电荷量 (未知)时,发现小球在垂直圆环平面的对称轴上处于平衡状态,如图所示.已知静电力常量为
(未知)时,发现小球在垂直圆环平面的对称轴上处于平衡状态,如图所示.已知静电力常量为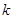 ,则有( )
,则有( ) 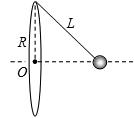
A.绳对小球的拉力 |
B.电荷量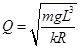 |
C.绳对小球的拉力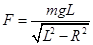 |
D.电荷量 |
下列说法正确的是
| A.运动越快的汽车越不容易停下来,是因为汽车运动得越快,惯性越大 |
| B.同一物体在地球上不同的位置受到的重力是不同的,所以它的惯性也随位置的变化而变化 |
| C.一个小球竖直上抛,抛出后能继续上升,是因为小球运动过程中受到了向上的推力 |
| D.物体的惯性大小只与本身的质量有关,质量大的物体惯性大,质量小的物体惯性小 |