题目内容
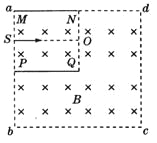
【题目】如图所示，边长为l的正方形abcd区域（含边界）内，存在着垂直于区域平面向内的匀强磁场，磁感应强度为B，带电平行金属板MN、PQ间形成了匀强电场（不考虑金属板在其他区域形成的电场）。MN放在ad边上，两板左端M、P恰在ab边上，金属板长度、板间距均为l/2，S为MP的中点，O为NQ的中点。一带负电的粒子（质量为m，电荷量的绝对值为q）从S点开始，刚好沿着直线S0运动，然后打在bc边的中点。（不计粒子的重力）
（1）求带电粒子的速度
。
（2）求电场强度E的大小。
（3）如果另一个质量为m、电荷量为q的带正电的粒子某一时刻从c点沿cd方向射入，在带负电的粒子打到bc中点之前与之相向正碰，求该带正电的粒子入射的速率v。
【答案】（1）
（2）
（3）
【解析】试题分析：（1）粒子水平离开0点并到达bc的中点，其运动轨迹如图所示，
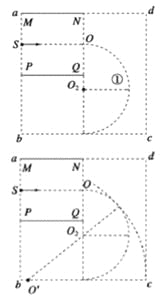
轨道半径
据
知，带电粒子的速度
。
（2）在正交的电磁场中，带电粒子受力平衡，则:qE=qv0B
解得电场强度：
（3）两粒子相向正碰，其轨迹相切，如图所示，设从c进入磁场的粒子轨道半径为r/,速率为v/，由几何关系知:
解得
由牛顿第二定律知：
解得:
练习册系列答案
相关题目
