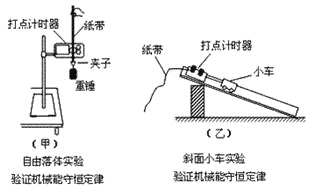
题目内容
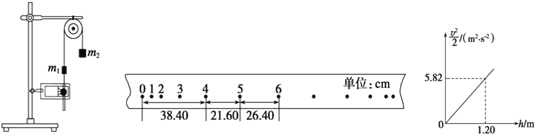
【题目】某物理课外小组利用图(a)中的装置探究物体加速度与其所受合外力之间的关系。图中,置于实验台上的长木板水平放置,其右端固定一轻滑轮;轻绳跨过滑轮,一端与放在木板上的小滑车相连,另一端可悬挂钩码。本实验中可用的钩码共有N=5个,每个质量均为0.010kg。实验步骤如下:
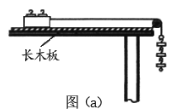
(1)将5个钩码全部放入小车中,在长木板左下方垫上适当厚度的小物快,使小车(和钩码)可以在木板上匀速下滑。
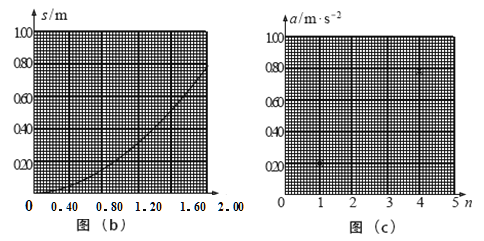
(2)将n(依次取n=1,2,3,4,5)个钩码挂在轻绳右端,其余N-n个钩码仍留在小车内;用手按住小车并使轻绳与木板平行。释放小车,同时用传感器记录小车在时刻t相对于其起始位置的位移s,绘制s-t图像,经数据处理后可得到相应的加速度a。
(3)对应于不同的n的a值见下表。n=2时的s-t图像如图(b)所示;由图(b)求出此时小车的加速度(保留2位有效数字),将结果填入下表。
n | 1 | 2 | 3 | 4 | 5 |
| 0.20 | 0.58 | 0.78 | 1.00 |
(4)利用表中的数据在图(c)中补齐数据点,并作出a-n图像。从图像可以看出:当物体质量一定时,物体的加速度与其所受的合外力成正比。
(5)利用a–n图像求得小车(空载)的质量为_______kg(保留2位有效数字,重力加速度取g=9.8 m·s–2)。
(6)若以“保持木板水平”来代替步骤(1),下列说法正确的是_______(填入正确选项前的标号)
A.a–n图线不再是直线
B.a–n图线仍是直线,但该直线不过原点
C.a–n图线仍是直线,但该直线的斜率变大
【答案】(3)0.39(4)如图(5)0.43~0.45(6)BC
【解析】
试题分析:(3)因为小车做初速度为0的匀加速直线运动,故将(2,0.78)代入![]() 可得
可得![]()
(4)根据描点法可得如图所示图线
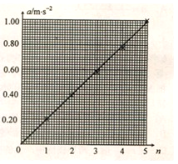
(5)根据牛顿第二定律可得nmg=(M+5m)a,代入数据得M=0.44kg
(6)若不平衡摩擦力,则满足nmg-μ1[M+(5-n)m]g=(M+5m)a的形式,所以a—n直线不过原点,但仍是直线,且斜率变大,BC正确;

【题目】如图所示是用光电门传感器测定小车瞬时速度的情景,轨道上a、c间距离恰等于小车长度,b是a、c中点。某同学采用不同的挡光片做了三次实验,并对测量精确度加以比较。挡光片安装在小车中点处,光电门安装在c点,它测量的是小车前端P抵达_______(选填“a”“b”或“c”)点时的瞬时速度;若每次小车从相同位置释放,记录数据如表格所示,那么测得瞬时速度较精确的值为_______m/s。
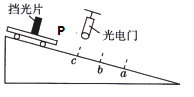
次序 | 挡光片宽/m | 挡光时间/s | 速度/(ms-1) |
1 | 0.080 | 0.036 | 2.22 |
2 | 0.040 | 0.020 | 2.00 |
3 | 0.020 | 0.0105 | 1.90 |