题目内容
 如图所示,轻且不可伸长的细绳悬挂质量为0.5kg 的小圆球,圆球又套在可沿水平方向移动的框架槽内,框架槽沿铅直方向,质量为0.2kg.自细绳静止于铅直位置开始,框架在水平力F=20N恒力作用下移至图中位置,此时细绳与竖直方向夹角30°.绳长0.2m,不计一切摩擦.则此过程中重力对小圆球做功为
如图所示,轻且不可伸长的细绳悬挂质量为0.5kg 的小圆球,圆球又套在可沿水平方向移动的框架槽内,框架槽沿铅直方向,质量为0.2kg.自细绳静止于铅直位置开始,框架在水平力F=20N恒力作用下移至图中位置,此时细绳与竖直方向夹角30°.绳长0.2m,不计一切摩擦.则此过程中重力对小圆球做功为分析:(1)根据上升的高度求出重力做功.
(2)对系统运用动能定理,抓住拉力做功、重力做功,结合小球和框架槽的速度关系,求出球和框架槽的速度大小.
(2)对系统运用动能定理,抓住拉力做功、重力做功,结合小球和框架槽的速度关系,求出球和框架槽的速度大小.
解答:解:(1)小球重力所做功为WG=-mgl(1-cosθ)=-0.5×10×0.2×(1-
)=-0.13J
(2)外力F做功WF=Flsinθ=20×0.2×
=2J
将小球和框架槽看作一个系统,则有系统动能定理:WF-WG=
m1vx2+
m2v2,其中m1、vx为小球的质量和小球此时的速度,m2、v为框架槽的质量和此时的速度.
由运动的分解得:v=vxcos30°
代入上述方程:2-0.13=
×0.5vx2+
×0.2×(vxcos30°)2
最后得:vx=2.39m/s.
故答案为:-0.13;2.39.
| ||
| 2 |
(2)外力F做功WF=Flsinθ=20×0.2×
| 1 |
| 2 |
将小球和框架槽看作一个系统,则有系统动能定理:WF-WG=
| 1 |
| 2 |
| 1 |
| 2 |
由运动的分解得:v=vxcos30°
代入上述方程:2-0.13=
| 1 |
| 2 |
| 1 |
| 2 |
最后得:vx=2.39m/s.
故答案为:-0.13;2.39.
点评:解决本题的关键知道小球和框架槽间的速度关系,对系统运用动能定理求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
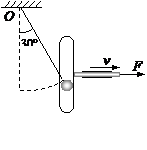

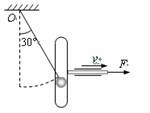 如图所示,轻且不可伸长的细绳悬挂质量为0.5kg 的小圆球,圆球又套在可沿水平方向移动的框架槽内,框架槽沿铅直方向,质量为0.2kg。自细绳静止于铅直位置开始,框架在水平力F=20N恒力作用下移至图中位置,此时细绳与竖直方向夹角30°。绳长0.2m,不计一切摩擦。
如图所示,轻且不可伸长的细绳悬挂质量为0.5kg 的小圆球,圆球又套在可沿水平方向移动的框架槽内,框架槽沿铅直方向,质量为0.2kg。自细绳静止于铅直位置开始,框架在水平力F=20N恒力作用下移至图中位置,此时细绳与竖直方向夹角30°。绳长0.2m,不计一切摩擦。