题目内容
【题目】北斗卫星导航系统是中国自行研制的全球卫星导航系统。如图所示，北斗卫星导航系统中的两颗工作卫星1、2均绕地心做顺时针方向的匀速圆周运动，轨道半径为r，某时刻两颗工作卫星分别位于同一圆轨道上的A、B两位置。已知地球表面附近的重力加速度为g，地球半径为R，不计卫星间的相互作用力。则以下判断中正确的是
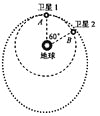
A. 卫星1向后喷气就一定能追上卫星2
B. 卫星1由位置A运动到位置B所需的时间为
C. 卫星1、2绕地球做匀速圆周运动的向心力大小一定相等
D. 若卫星1由圆轨道上的位置A变轨能进入椭圆轨道，则卫星1在圆轨道上经过位置A的加速度小于在椭圆轨道上经过位置A的加速度
【答案】B
【解析】
卫星1向后喷气时需要加速，所需要的向心力增大，而万有引力不变，卫星将做离心运动，轨道半径增大，不可能追上卫星2，A错误；卫星做圆周运动，由万有引力提供向心力，
①，根据地球表面万有引力等于重力列出等式
②，由①②得
，卫星1由位置A运动到位置B所需的时间为
，B正确；由于卫星甲和卫星乙的质量不一定相等，所以地球对两颗卫星的万有引力大小不一定相等，C错误；根据万有引力提供向心力，有
，由于卫星1在圆轨道上经过位置A的轨道半径等于在椭圆轨道上经过位置A的轨道半径，故两次情况下加速度相等，D错误．
练习册系列答案
阅读快车系列答案
相关题目
