题目内容
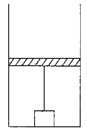
【题目】如图所示,开口向上、放在地面上的气缸内用活塞封闭一定质量的气体,活塞的质量为m,横截面的面积为S。一质量为2m的物块放在缸底,用细线(不可伸长)与活塞相连接且细线刚好拉直,这时缸内气体的温度为T0,大气压强为P0,不计活塞与缸壁间的摩擦,现对缸内气体缓慢加热,重力加速度为g。
(i)当缸底物块对缸底的压力刚好为零时,缸内气体温度T1为多大?
(ⅱ)当缸内气体体积为原来的1.2倍时,缸内气体温度是多少?若此时细线断了,细线断开的一瞬问,活塞的加速度多大?
【答案】(1)![]() ;(2)
;(2)![]() ,2g
,2g
【解析】
(1)当缸底物块对缸底的压力刚好为零时,选择活塞和重物的整体进行受力分析,列出平衡方程,封闭气体发生等容变化,对封闭气体运用查理定律,即可求出缸内气体温度T1为多大;
(2)继续缓慢加热,气体发生等压变化,当缸内气体体积为原来1.2倍时,利用盖-吕萨克定律即可求出此时缸内气体温度;若此时细线断了,绳的拉力消失,利用牛顿第二定律,即可求出此时活塞的加速度.
(i)缸内气体的温度为T0时,缸内气体的压强p=p0+![]()
当缸底物块对缸底的压力刚好为零时,缸内气体压强p1=p0+![]()
气体发生等容变化,则根据查理定律有![]()
解得:T1=![]()
(ii)当缸内气体体积为原来的1.2倍时,设气体的温度为T2,从温度T1变到温度T2,此过程气体发生的是等压变化,根据盖-吕萨克定律有![]()
解得:T2=![]()
此时细线断了,当细线断开的一瞬间,根据牛顿第二定律有(p2-p)S=ma
解得a=2g

练习册系列答案
相关题目