题目内容
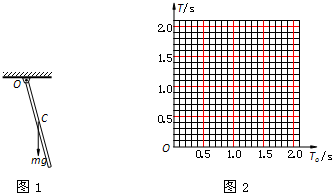 (2006?青浦区模拟)学过单摆的周期公式以后,物理兴趣小组的同学们对钟摆产生了兴趣,老师建议他们先研究用厚度和质量分布均匀的长木条(如一把米尺)做成的摆(这种摆被称为复摆),如图1所示.让其在竖直平面内做小角度摆动,C 点为重心,木条长为 L,周期用 T 表示.
(2006?青浦区模拟)学过单摆的周期公式以后,物理兴趣小组的同学们对钟摆产生了兴趣,老师建议他们先研究用厚度和质量分布均匀的长木条(如一把米尺)做成的摆(这种摆被称为复摆),如图1所示.让其在竖直平面内做小角度摆动,C 点为重心,木条长为 L,周期用 T 表示.甲同学猜想:复摆的周期应该与木条的质量有关.
乙同学猜想:复摆的摆长应该是悬点到重心的距离 L/2.
丙同学猜想:复摆的摆长应该大于 L/2.理由是:若 OC 段看成细线,线栓在C处,
C点以下部分的重心离O点的距离显然大于L/2.
为了研究以上猜想是否正确,同学们进行了下面的实验探索:
(1)把两个相同的长木条完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个长木条摆动时的周期相同,重做多次仍有这样的特点.则证明了甲同学的猜想是
错误
错误
的(选填“正确”或“错误”).(2)用 To 表示木条长为 L 的复摆看成摆长为 L/2 单摆的周期计算值(To=2π
|
| 板长L(cm) | 25 | 50 | 80 | 100 | 120 | 150 |
| 周期计算值To/(s) | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
| 周期测量值T/(s) | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
大于
大于
L/2 (选填“大于”、“小于”或“等于”).(3)为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标如图2所示.请在坐标纸上作出 T-To图线,并根据图象中反映出的规律求出
| L等 |
| L/2 |
1.16
1.16
(结果保留三位有效数字,其中 L等 是木条长为L时的等效摆长.T=2π
|
分析:(1)根据复摆的周期与质量有无关系,判断甲同学的猜想是否正确.
(2)根据表格的数据由单摆的周期公式分析复摆的等效摆长与
的关系.
(3)用描点作图法作出T-To图线.由图线的斜率求出
.
(2)根据表格的数据由单摆的周期公式分析复摆的等效摆长与
| L |
| 2 |
(3)用描点作图法作出T-To图线.由图线的斜率求出
| ||||
|
解答:解:(1)把两个相同的长木条完全重叠在一起,构成的复摆质量大于单个长木条复摆的质量,而两者周期相同,说明复摆的周期与质量无关,证明甲同学的猜想是错误的.
(2)由表格看出,周期测量值T大于周期计算值To,由单摆的周期公式T=2π
得知,复摆的等效摆长大于
.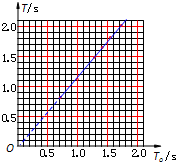
(3)用描点作图法作出T-To图线如图所示,由数学知识求得:图线的斜率k=
=1.10,则由T=2π
,T0=2π
得,
=1.10.
故答案为:
(1)错误;
(2)大于;
(3)在坐标纸上作出 T-To图线如图所示.1.10.
(2)由表格看出,周期测量值T大于周期计算值To,由单摆的周期公式T=2π
|
| L |
| 2 |

(3)用描点作图法作出T-To图线如图所示,由数学知识求得:图线的斜率k=
| T |
| T0 |
|
|
| ||||
|
故答案为:
(1)错误;
(2)大于;
(3)在坐标纸上作出 T-To图线如图所示.1.10.
点评:本题题干较长,首先考查快速获取信息的能力;其次考查知识的迁移能力,用单摆的原理来理解、分析复摆的原理.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 (2006?青浦区模拟)A:如图所示,一根粗细均匀一端封闭的玻璃管,注入60mm的水银柱,水平放置时封闭端空气柱与开口端气柱长均为140mm.若将管缓慢转动,然后开口向下竖直插入水银槽中,使得封闭端气柱长133mm.外界大气压强Po=760mmHg,求水银槽中水银进入玻璃管开口端的长度△h.
(2006?青浦区模拟)A:如图所示,一根粗细均匀一端封闭的玻璃管,注入60mm的水银柱,水平放置时封闭端空气柱与开口端气柱长均为140mm.若将管缓慢转动,然后开口向下竖直插入水银槽中,使得封闭端气柱长133mm.外界大气压强Po=760mmHg,求水银槽中水银进入玻璃管开口端的长度△h. (2006?青浦区模拟)将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示,根据此图提供的信息作出以下判断( )
(2006?青浦区模拟)将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示,根据此图提供的信息作出以下判断( ) (2006?青浦区模拟)一九二三年美国物理学家迈克耳逊用旋转棱镜法较准确的测出了光速,其过程大致如下,选择两个距离已经精确测量过的山峰(距离为L),在第一个山峰上装一个强光源S,由它发出的光经过狭缝射在八面镜的镜面1上,被反射到放在第二个山峰的凹面镜B上,再由凹面镜B反射回第一个山峰,如果八面镜静止不动,反射回来的光就在八面镜的另外一个面3上再次反射,经过望远镜,进入观测者的眼中.(如图所示) 如果八面镜在电动机带动下从静止开始由慢到快转动,当八面镜的转速为ω时,就可以在望远镜里重新看到光源的像,那么光速等于( )
(2006?青浦区模拟)一九二三年美国物理学家迈克耳逊用旋转棱镜法较准确的测出了光速,其过程大致如下,选择两个距离已经精确测量过的山峰(距离为L),在第一个山峰上装一个强光源S,由它发出的光经过狭缝射在八面镜的镜面1上,被反射到放在第二个山峰的凹面镜B上,再由凹面镜B反射回第一个山峰,如果八面镜静止不动,反射回来的光就在八面镜的另外一个面3上再次反射,经过望远镜,进入观测者的眼中.(如图所示) 如果八面镜在电动机带动下从静止开始由慢到快转动,当八面镜的转速为ω时,就可以在望远镜里重新看到光源的像,那么光速等于( ) (2006?青浦区模拟)B:如图中竖直方向的平行线表示匀强电场的电场线,但未标明方向.电场中有一个带正电荷的微粒,电量为10-5C,若该带电微粒仅受电场力的作用,从M点运动到N点时,动能减少了10-3 J,则该电荷运动轨迹应为虚线
(2006?青浦区模拟)B:如图中竖直方向的平行线表示匀强电场的电场线,但未标明方向.电场中有一个带正电荷的微粒,电量为10-5C,若该带电微粒仅受电场力的作用,从M点运动到N点时,动能减少了10-3 J,则该电荷运动轨迹应为虚线