题目内容
12.如图甲所示,以O为原点建立Oxy平面直角坐标系.两平行极板P、Q垂直于y轴且关于x轴对称放置,极板长度和极板间距均为l,第一、四象限有方向垂直于Oxy平面向里的匀强磁场.紧靠极板左侧的粒子源沿x轴向右连续发射带电粒子,已知粒子的质量为m、电荷量为+q、速度为v0、重力忽略不计,两板间加上如图乙所示的扫描电压(不考虑极板边缘的影响).带电粒子恰能全部射入磁场.每个粒子穿过平行板的时间极短,穿越过程可认为板间电压不变;不考虑粒子间的相互作用.
(1)求扫描电压的峰值U0的大小.
(2)已知射入磁场的粒子恰好全部不再返回板间,匀强磁场的磁感应强度B应为多少?所有带电粒子中,从粒子源发射到离开磁场的最短时间是多少?
分析 (1)粒子在电场中做类平抛运动,由题意可知,粒子的运动情况,根据运动的合成与分解可求得的加电压的峰值;
(2)粒子在磁场中做圆周运动,由洛仑兹力充当向心力以及几何关系可求得磁感应强度;
(3)粒子从上边缘飞出时时间最短,则由运动过程可求得各段内所经历的时间,则可求得总时间.
解答  解:(1)所加扫描电压达到峰值时,粒子在电场中的偏转位移为$\frac{l}{2}$,
解:(1)所加扫描电压达到峰值时,粒子在电场中的偏转位移为$\frac{l}{2}$,
粒子在电场中做类平抛运动,运动加速度为a=$\frac{q{U}_{0}}{ml}$,时间为t=$\frac{l}{{v}_{0}}$
在电场中的偏转位移 y=$\frac{1}{2}$at2=$\frac{q{U}_{0}l}{2m{v}_{0}^{2}}$=$\frac{l}{2}$
故所加扫描电压的峰值为 U0=$\frac{m{v}_{0}^{2}}{q}$
(2)设粒子从电场射出时的速度偏转角为θ,射入磁场时的速度为v=$\frac{{v}_{0}}{cosθ}$
粒子在磁场中做圆周运动时,洛伦兹力提供向心力qvB=m$\frac{{v}^{2}}{R}$
粒子在磁场中射入与射出点间的距离为△y=2Rcosθ
联立得△y=$\frac{2m{v}_{0}}{qB}$,即所有粒子在磁场中射入与射出点间距离相同
依题意,从下边缘射出电场的粒子在磁场中做圆周运动后刚好到达电场上边缘,
即△y=l
故匀强磁场的磁感应强度为B=$\frac{2m{v}_{0}}{ql}$
从电场上边缘射出的粒子整个过程运动时间最短,
粒子速度偏转角正切值tanα=$\frac{at}{{v}_{0}}$=$\frac{q{U}_{0}l}{m{v}_{0}^{2}l}$=1
故α=45°
粒子在电场中运动的时间为t1=$\frac{l}{{v}_{0}}$
粒子在磁场中运动的最短时间为t1=$\frac{T}{4}$=$\frac{πm}{2qB}$
故带电粒子从发射到离开磁场的最短时间是t=t1+t2=$\frac{l}{{v}_{0}}$(1+$\frac{π}{4}$)
答:(1)扫描电压的峰值U0的大小为$\frac{m{v}_{0}^{2}}{q}$;
(2)已知射入磁场的粒子恰好全部不再返回板间,匀强磁场的磁感应强度B应为$\frac{2m{v}_{0}}{ql}$;所有带电粒子中,从粒子源发射到离开磁场的最短时间是$\frac{m{v}_{0}^{2}}{q}$
点评 本题考查带电粒子在电场和磁场中的运动规律,要注意认真审题,明确题意才能正确分析物理过程,进而确定正确的物理规律求解!如本题中明确说明通过时间极短,粒子通过时电场不变,故粒子即可不同电压下进行加速!

| A. | 在原子核中,结合能越大表示原子核中的核子结合的越牢固 | |
| B. | 原子从基态跃迁到其它轨道时,电子的动能减小,势能增大 | |
| C. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中减少了32个中子 | |
| D. | 一束光折射到某种金属上不能发生光电效应,可能是因为该电光频率太小 | |
| E. | 用加热、加压或改变其化学状态的方法都不能改变原子核衰变的半衰期 |
| A. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{{r}_{2}}^{2}}{{{r}_{1}}^{2}}$ | B. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}_{1}}{{r}_{2}}$ | C. | $\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | D. | $\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{\frac{{{r}_{2}}^{3}}{{{r}_{1}}^{3}}}$ |
| A. | 安培发现了电流的磁效应 | |
| B. | 库仑通过扭秤实验发现了电流的热效应 | |
| C. | 奥斯特发现了磁场产生电流的条件和规律 | |
| D. | 麦克斯建立了电磁场理论并预言了电磁波的存在 |
 如图所示,无磁场时,电视显像管中的水平向右运动的电子束打在荧光屏正中的O点,要使电子束在竖直方向向上偏转打在P点,则管颈处偏转线圈所提供的磁场方向应该是( )
如图所示,无磁场时,电视显像管中的水平向右运动的电子束打在荧光屏正中的O点,要使电子束在竖直方向向上偏转打在P点,则管颈处偏转线圈所提供的磁场方向应该是( )| A. | 垂直纸面向外 | B. | 水平向右 | C. | 垂直纸面向里 | D. | 竖直向上 |
 质量为m的汽车在平直路面上启动,启动过程的速度图象如图所示,从t1时刻起汽车的功率保持不变,整个运动过程中汽车所受阻力恒为Ff,则( )
质量为m的汽车在平直路面上启动,启动过程的速度图象如图所示,从t1时刻起汽车的功率保持不变,整个运动过程中汽车所受阻力恒为Ff,则( )| A. | t1~t2时间内,汽车的平均速度等于$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| B. | 0~t1时间内,汽车的牵引力等于m$\frac{{v}_{1}}{{t}_{1}}$ | |
| C. | t1~t2时间内,汽车的功率等于(m$\frac{{v}_{1}}{{t}_{1}}$+Ff)v1 | |
| D. | 汽车运动的过程中最大速度v2=$\frac{m{v}_{1}^{2}}{{F}_{f}{t}_{1}}$ |
 在地面附近的竖直平面内,有如图所示足够大的电磁场区域,虚线MN上方,有电场强度为E1的竖直向下的匀强电场,虚线与水平面的夹角θ=45°,虚线下方有电场强度为E2的竖直向上的匀强电场和垂直于竖直纸面向里的匀强磁场,已知E2=E1,匀强磁场的磁感应强度大小B=0.1T,从图中A点沿水平方向同时向左发射两个比荷相同的带正电质点甲和乙,比荷$\frac{q}{m}$=100c/kg,甲,乙质点的初速度分別v1=10m/s和v2=20m/s,它们进入虚线下方后均恰好做匀速圆周运动,经下方电磁场区域偏转后到达虚线MN上的P、Q两点,(P、Q两点图中未标出)求:
在地面附近的竖直平面内,有如图所示足够大的电磁场区域,虚线MN上方,有电场强度为E1的竖直向下的匀强电场,虚线与水平面的夹角θ=45°,虚线下方有电场强度为E2的竖直向上的匀强电场和垂直于竖直纸面向里的匀强磁场,已知E2=E1,匀强磁场的磁感应强度大小B=0.1T,从图中A点沿水平方向同时向左发射两个比荷相同的带正电质点甲和乙,比荷$\frac{q}{m}$=100c/kg,甲,乙质点的初速度分別v1=10m/s和v2=20m/s,它们进入虚线下方后均恰好做匀速圆周运动,经下方电磁场区域偏转后到达虚线MN上的P、Q两点,(P、Q两点图中未标出)求:



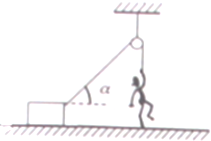 如图所示,人的质量M=80kg,粗糙水平面上物体质量m=30kg,当人用F=100N的力向下拉绳子时,人与物体均处于静止状态,已知绳与水平面成α=60°角,(取g=10m/s2).求:
如图所示,人的质量M=80kg,粗糙水平面上物体质量m=30kg,当人用F=100N的力向下拉绳子时,人与物体均处于静止状态,已知绳与水平面成α=60°角,(取g=10m/s2).求: