题目内容
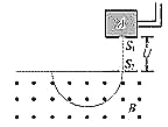
【题目】质谱仪是分析同位素的重要工具。如图所示,设质量为![]() 、电荷量为q的离子,从容器A下方的小孔
、电荷量为q的离子,从容器A下方的小孔![]() 不断飘入加速电场,其初速度可视为零,然后经过小孔
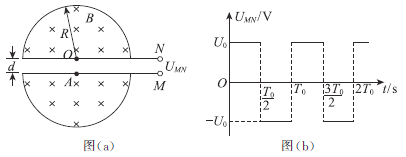
不断飘入加速电场,其初速度可视为零,然后经过小孔![]() 垂直于磁场方向进入磁感应强度为B的匀强磁场中,做半径为R的匀速圆周运动。离子行进半个圆周后离开磁场并被收集,不考虑离子重力及离子间的相互作用。
垂直于磁场方向进入磁感应强度为B的匀强磁场中,做半径为R的匀速圆周运动。离子行进半个圆周后离开磁场并被收集,不考虑离子重力及离子间的相互作用。
(1)求加速电场的电压U;
(2)若容器A中有电荷量同为q、质量分别为![]() 和
和![]() 的同种元素的两种离子(设
的同种元素的两种离子(设![]() >
>![]() ),它们经电场加速后进入磁场中会发生分离.某次实验时加速电压的大小在U±ΔU范围内发生有微小变化。
),它们经电场加速后进入磁场中会发生分离.某次实验时加速电压的大小在U±ΔU范围内发生有微小变化。![]() 应在什么范围内才能使这两种离子在磁场中运动的轨迹不发生交叠?
应在什么范围内才能使这两种离子在磁场中运动的轨迹不发生交叠?
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设离子经电场加速度时的速度为v,由动能定理及向心力公式即可求解;
(2)根据向心力公式求出半径R的表达式,进而表示出m离子在磁场中最大半径和离子m′在磁场中最小半径,要使两种离子在磁场中运动的轨迹不发生交叠,则m离子在磁场中最大半径小于m′离子在磁场中最小半径,进而即可求解.
(1)设离子经电场加速后进入磁场时的速度为v,由动能定理得:qU=![]() mv2…①
mv2…①
离子在磁场中做匀速圆周运动,所受洛伦兹力提供向心力,有:![]() …②
…②
由①②式解得:![]() …③
…③
(2)由前面得: ![]()
电压变化时,质量较小的m离子在磁场中运动的最大半径为: ![]()
质量较大的m′ 离子在磁场中运动的最小半径为: ![]()
两种离子在磁场中运动的轨迹不发生交叠的条件为: Rmax<R′min
即:![]() 解得:
解得: ![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目