题目内容
16．
在如图所示的电路中，电容器的电容为C，现将滑动变阻器R的滑片稍向上移动一些，电压表示数变化量的绝对值为△U，电容器电量变化量的绝对值为△Q．下列说法正确的是（ ）| A． | △Q一定大于C•△U | B． | 灯泡L2一定变亮 | ||
| C． | 电源输出功率一定减小 | D． | 电容器的带电量一定增大 |
分析 将滑动变阻器R的滑片稍向上移动时，分析变阻器接入电路的电阻变化情况，得到总电阻的变化情况，判断路端电压的变化，从而得到电容器板间电压的变化量与电压表示数变化量的关系，从而分析△Q与C•△U的关系．根据并联部分电压的变化分析灯泡L2亮度的变化．根据内外电阻的关系，分析电源输出功率的变化．由Q=CU分析电容器带电量的变化．
解答 解：A、将滑动变阻器R的滑片稍向上移动时，变阻器接入电路的电阻变小，外电路总电阻变小，总电流变大，电源的内电压变大，则路端电压变小．总电流变大，灯泡L1的电压变大，即电压表的示数变大．根据路端电压等于灯泡L1的电压与右侧并联部分电压之和，可知，右侧并联部分电压变小，由于路端电压变小，所以右侧并联部分电压减小量大于灯泡L1电压的增加量，所以电容器电压的变化量绝对值大于△U，因此电容器电量变化量的绝对值为△Q一定大于C•△U．故A正确．
B、右侧并联部分电压变小，灯泡L2的电压变小，则灯泡L2一定变暗，故B错误．
C、由于电源的内外电阻关系未知，所以不能判断电源输出功率如何变化，故C错误．
D、电容器板间电压变小，则电容器的带电量一定减小，故D错误．
故选：A
点评 本题是电路的动态分析问题，关键抓住电动势和内阻不变，结合闭合电路欧姆定律进行分析，以及知道外电阻等于内电阻时，输出功率最大．根据内外电阻的关系才能分析电源输出功率的变化情况．
练习册系列答案
阅读快车系列答案
相关题目
9．
如图所示，光滑绝缘斜面的倾角为θ，在斜面上放置一个矩形线框abcd，ab边的边长为l1，bc的边长为l2，线框的质量m，总电阻为R，线框通过细线与重物相连（细线与斜面平行）．重物质量为M，斜面上ef线（ef平行于gh且平行于底边）的上方有垂直于斜面向上的匀强磁场（fh远大于l2），如果线框从静止开始运动，且进入磁场的最初一段时间是做匀速运动，假设斜面足够长，运动过程总ab边始终与ef平行，则（ ）
如图所示，光滑绝缘斜面的倾角为θ，在斜面上放置一个矩形线框abcd，ab边的边长为l1，bc的边长为l2，线框的质量m，总电阻为R，线框通过细线与重物相连（细线与斜面平行）．重物质量为M，斜面上ef线（ef平行于gh且平行于底边）的上方有垂直于斜面向上的匀强磁场（fh远大于l2），如果线框从静止开始运动，且进入磁场的最初一段时间是做匀速运动，假设斜面足够长，运动过程总ab边始终与ef平行，则（ ）| A． | 线框abcd进入磁场前运动的加速度为$\frac{Mg-mgsinθ}{m}$ | |
| B． | 线框在进入磁场过程中的运动速度v=$\frac{（Mg-mgsinθ）R}{{B}^{2}{l}_{1}^{2}}$ | |
| C． | 线框做匀速运动的时间为$\frac{{B}^{2}{l}_{1}^{2}{l}_{2}}{（Mg-mgsinθ）R}$ | |
| D． | 线框进入磁场过程中产生的焦耳热Q=（Mg-mgsinθ）l1 |
7．
一个人在岸上以恒定的速度v通过定滑轮收拢连接在船上的牵引绳．当船运动到如图所示位置时，绳子与水平方向的夹角为α，则船的运动速度为（ ）
一个人在岸上以恒定的速度v通过定滑轮收拢连接在船上的牵引绳．当船运动到如图所示位置时，绳子与水平方向的夹角为α，则船的运动速度为（ ）| A． | v | B． | vcosα | C． | $\frac{v}{cosα}$ | D． | vtanα |
4．
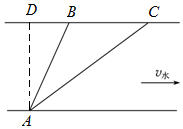如图所示，甲登陆舰船头垂直海岸从A点出发，沿路径AC在对岸C点登陆．乙登陆舰船头垂直海岸从A点出发，沿路径AB在对岸B点登陆．已知水流速度恒定，路径AC与海岸的夹角为45°，则下列说法正确的是（ ）
如图所示，甲登陆舰船头垂直海岸从A点出发，沿路径AC在对岸C点登陆．乙登陆舰船头垂直海岸从A点出发，沿路径AB在对岸B点登陆．已知水流速度恒定，路径AC与海岸的夹角为45°，则下列说法正确的是（ ）| A． | 甲登陆舰的航速大 | |
| B． | 甲登陆舰航行所用时间较短 | |
| C． | 两登陆舰航行所用时间相等 | |
| D． | 无论船头方向如何，甲登陆舰都无法在A点正对岸D点登陆 |
11．如图甲所示，轻弹簧竖直固定在水平面上处于自由状态，一质量为m=0.2kg的小球，从弹簧上端某高度处自由下落，从它接触弹簧到弹簧压缩至最短的过程中（弹簧在弹性限度内），其速度u和弹簧压缩量△x之间的函数图象如图乙所示，其中A为曲线的最高点，小球和弹簧接触瞬间机械能损失不计，取g=10m/s2，则（ ）
| A． | 当△x=0.1m时，小球处于失重状态 | |
| B． | 小球在最低点时的加速度大于10m/s2 | |
| C． | 从接触弹簧到压缩至最短的过程中，小球的机械能守恒 | |
| D． | 小球从速度最大到压缩至最短，弹簧弹性势能增加量为3.621J |
1．
如图A中水平放置的U形光滑金属导轨NMPQ，MN接有电键K，导轨宽度为L，其电阻不计，在左侧边长为L的正方形区域存在方向竖直向上磁场B，其变化规律如图B所示，中间一段没有磁场，右侧一段区域存在方向竖直向下的匀强磁场，其磁感应强度为B0，在该段导轨之间放有质量为m、电阻为R、长为L的金属棒ab，若在图B所示的$\frac{{t}_{0}}{2}$时刻关闭电键K，则在这一瞬间（ ）
如图A中水平放置的U形光滑金属导轨NMPQ，MN接有电键K，导轨宽度为L，其电阻不计，在左侧边长为L的正方形区域存在方向竖直向上磁场B，其变化规律如图B所示，中间一段没有磁场，右侧一段区域存在方向竖直向下的匀强磁场，其磁感应强度为B0，在该段导轨之间放有质量为m、电阻为R、长为L的金属棒ab，若在图B所示的$\frac{{t}_{0}}{2}$时刻关闭电键K，则在这一瞬间（ ）| A． | 金属棒ab中的电流方向为由a流向b | |
| B． | 金属棒ab中的电流大小为$\frac{L{B}_{0}}{{t}_{0}R}$ | |
| C． | 金属棒ab所受安培力方向水平向右 | |
| D． | 金属棒ab的加速度大小为$\frac{{L}^{3}{B}_{0}^{2}}{m{t}_{0}R}$ |
，则驾驶员允许的最长反映时间为
的速度匀速上升，升至距离地面64m高处从气球上掉下一个物体，问：