题目内容
12. 一棱镜的截面为直角三角形ABC,∠A=30°,直角边BC=a,棱镜材料的折射率为n=$\sqrt{2}$,在此截面所在的平面内,一条光线以45°的入射角从直角边AC的中点M射入棱镜,不考虑光线沿原路返回的情况.求:
一棱镜的截面为直角三角形ABC,∠A=30°,直角边BC=a,棱镜材料的折射率为n=$\sqrt{2}$,在此截面所在的平面内,一条光线以45°的入射角从直角边AC的中点M射入棱镜,不考虑光线沿原路返回的情况.求:光线从棱镜射出的点到B的距离(直接写结果不给分).
分析 光线以45°的入射角时,先根据折射定律求出光线在AC面的折射角r.根据几何知识确定光线在AB面上的入射角.由sinC=$\frac{1}{n}$求出临界角C,判断在AB面上能否发生全反射,画出光路图,求出光线从棱镜射出点的位置离B点的距离.
解答  解:设光线在AC面上的入射角为i,折射角为r.
解:设光线在AC面上的入射角为i,折射角为r.
由折射定律 n=$\frac{sini}{sinr}$
可得光线第一次折射角为 r=30°
光线射到AB界面上D点时,入射角等于60°
而临界角的正弦值sinC=$\frac{1}{n}$=$\frac{\sqrt{2}}{2}$<$\frac{\sqrt{3}}{2}$,则临界角C<60°
则光线在AB界面上发生全反射,光线垂直BC面从E点射出棱镜.
由几何关系可知,
MD=$\frac{\sqrt{3}}{2}$a,AD=1.5a,DB=2a-AD=0.5a
则光线出射点到B的距离为:
EB=DBcos60°=$\frac{1}{4}$a
答:光线从棱镜射出的点到B的距离是$\frac{1}{4}$a.
点评 本题是折射定律、全反射和几何知识的综合应用,作出光路图,判断能否发生全反射是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列说法中正确的是( )
| A. | 光电效应实验揭示了光的粒子性 | |
| B. | 原子核发生一次β衰变,该原子核外就失去一个电子 | |
| C. | 原子核放出β粒子后,转变成的新核所对应的元素是原来的同位素 | |
| D. | 玻尔在研究原子结构中引进了量子化的观念 |
3.大气气流额升降运动会造成不同高度的温度变化,致使气象万变,万米高空的气温往往在-50℃以下,在研究大气现象时可把温度、压强相同的一部分气体作为研究对象,叫做气团.气团直径可达几千米,由于气团很大,边缘部分与外界的热交换对整个气团没有明显影响,可以忽略不计.用气团理论解释高空气温很低的原因,是因为地面的气团上升到高空的过程中( )
| A. | 剧烈膨胀,同时大量对外放热,使周围温度降低 | |
| B. | 剧烈收缩,同时从周围吸收大量热量,使周围温度降低 | |
| C. | 剧烈膨胀,气团对外做功,内能大量减少导致温度降低 | |
| D. | 剧烈收缩,外界对气团做功,故周围温度降低 |
20.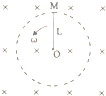 如图所示,在磁感应强度为B的匀强磁场中,一长为L的OM金属导棒,以一端点O为轴,以角速度ω逆时针垂直切割磁感线运动,关于O、M两点电势差的大小,下列说法正确的是( )
如图所示,在磁感应强度为B的匀强磁场中,一长为L的OM金属导棒,以一端点O为轴,以角速度ω逆时针垂直切割磁感线运动,关于O、M两点电势差的大小,下列说法正确的是( )
 如图所示,在磁感应强度为B的匀强磁场中,一长为L的OM金属导棒,以一端点O为轴,以角速度ω逆时针垂直切割磁感线运动,关于O、M两点电势差的大小,下列说法正确的是( )
如图所示,在磁感应强度为B的匀强磁场中,一长为L的OM金属导棒,以一端点O为轴,以角速度ω逆时针垂直切割磁感线运动,关于O、M两点电势差的大小,下列说法正确的是( )| A. | $\frac{1}{4}$BL2ω | B. | $\frac{1}{2}$BL2ω | C. | BL2ω | D. | 2BL2ω |
17.某玩具手枪将一颗子弹射出,t1时刻子弹的速度方向与水平方向成θ1=30°,t2时刻子弹的位移方向与水平方向成θ2=60°,若忽略空气阻力,则在t1•t2时刻子弹在竖直方向的速度之比为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.当汽车的发动机功率一定时,则( )
| A. | 要增大汽车牵引力,就必须增大其速度 | |
| B. | 要增大汽车牵引力,就必须减小其速度 | |
| C. | 增大汽车的速度,其牵引力一定会变大 | |
| D. | 增大汽车速度,其牵引力一定会不变 |

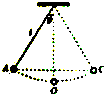 把一个小球用细线悬挂起来,就成为一个摆,如图所示,摆长为l,最大摆角为θ,如图阻力可以忽略,小球运动到最低位置时的速度是多少?
把一个小球用细线悬挂起来,就成为一个摆,如图所示,摆长为l,最大摆角为θ,如图阻力可以忽略,小球运动到最低位置时的速度是多少? 如图所示,A、B两物块用一根轻绳跨过定滑轮相连,不带电的B、C通过一根轻弹簧栓接在一起,且处于静止状态,其中A带负电,电荷量大小为q.质量为2m的A静止于斜面的光滑部分(斜面倾角为37°,其上部分光滑,下部分粗糙且足够长,粗糙部分的摩擦系数为μ=tan30°,上方有一个平行于斜面向下的匀强电场),通过细绳与B相连接,此时与B相连接的轻弹簧恰好无形变.弹簧劲度系数为k.B、C质量相等,均为m,不计滑轮的质量和摩擦,重力加速度为g.
如图所示,A、B两物块用一根轻绳跨过定滑轮相连,不带电的B、C通过一根轻弹簧栓接在一起,且处于静止状态,其中A带负电,电荷量大小为q.质量为2m的A静止于斜面的光滑部分(斜面倾角为37°,其上部分光滑,下部分粗糙且足够长,粗糙部分的摩擦系数为μ=tan30°,上方有一个平行于斜面向下的匀强电场),通过细绳与B相连接,此时与B相连接的轻弹簧恰好无形变.弹簧劲度系数为k.B、C质量相等,均为m,不计滑轮的质量和摩擦,重力加速度为g.