题目内容
7.如图甲所示,两根足够长、电阻不计的光滑平行金属导轨相距L1=1m,导轨平面与水平面成θ=30°角,上端连接阻值R=1.5Ω的电阻,质量为m=0.2kg,阻值r=0.5Ω的金属棒ab放在两导轨上,距离导轨最上端为L2=4m,棒与导轨垂直并保持良好接触.整个装置处于一个匀强磁场中,该匀强磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图乙所示,为保持ab棒静止,在棒上施加了一平行于导轨平面的外力F.g=10m/s2.求:(1)当t=2s时,外力F1的大小;
(2)当t=3s时的瞬间,外力F2的大小和方向;
(3)请 图丙中画出前4s外力F随时间变化的图象(规定F方向沿斜面向上为正).

分析 (1)在0-3s时间内B均匀增大,回路中产生恒定的感应电流,由法拉第电磁感应定律求感应电动势,由闭合电路欧姆定律得到电流.根据ab棒静止,受力平衡,由平衡条件求解外力的大小.
(2)由平衡条件求解外力F2的大小.
(3)0-3s内,由平衡条件得到F与t的关系式.在3-4s内,B不变,没有感应电流产生,ab不受安培力,再由平衡条件求得F,即可画出图象.
解答 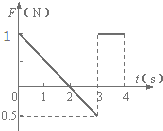 解:(1)当t=2s时,回路中产生的感应电动势:
解:(1)当t=2s时,回路中产生的感应电动势:
E=$\frac{△B}{△t}$L1L2=$\frac{1.5}{3}$×1×4V=2V
电流:I=$\frac{E}{R+r}$=$\frac{2}{1.5+0.5}$A=1A
由楞次定律判断可知,ab所受的安培力沿轨道向上;
ab棒保持静止,受力平衡,设外力沿轨道向上,则由平衡条件有:
mgsin30°-B2IL1-F1=0
可解得外力:F1=0
(2)当t=3s时的瞬间,设此时外力沿轨道向上,根据平衡条件得:F2+B3IL1-mg sin30°=0
解得:F2=-0.5N,负号说明外力沿斜面向下.
(3)规定F方向沿斜面向上为正,在0-3s内,根据平衡条件有:
mgsin30°-BIL1-F=0而B=0.5t(T)
则得:F=1-0.5t(N)
当t=0时刻,F=1N.
在3-4s内,B不变,没有感应电流产生,ab不受安培力,则由平衡条件得:F=mgsin30°=1N
画出前4s外力F随时间变化的图象如图所示.
答:(1)当t=2s时,外力F1的大小是0;
(2)当t=3s时的瞬间,外力F2的大小为0.5N,方向沿斜面向下;
(3)画出前4s外力F随时间变化的图象如图所示.
点评 本题是电磁感应与力学知识、电路等知识的综合,解决本题的关键掌握法拉第电磁感应定律E=n$\frac{△B}{△t}$S、导体棒切割产生的感应电动势E=BLv、安培力公式F=BIL和平衡条件.

 天天练口算系列答案
天天练口算系列答案 如图所示,两根长直导线竖直平行固定放置,且与水平固定放置的光滑绝缘杆MN分别交于c、d两点,点o是cd的中点,杆MN上a、b两点关于o点对称.两导线均通有大小相等、方向向上的电流,已知长直导线在周围某点产生磁场的磁感应强度与电流成正比、与该点到导线的距离成反比.一带正电的小球穿在杆上,以初速度v0从a点出发沿杆运动到b点.在a、b、o三点杆对小球的支持力大小分别为Fa、Fb、Fo.下列说法可能正确的是( )
如图所示,两根长直导线竖直平行固定放置,且与水平固定放置的光滑绝缘杆MN分别交于c、d两点,点o是cd的中点,杆MN上a、b两点关于o点对称.两导线均通有大小相等、方向向上的电流,已知长直导线在周围某点产生磁场的磁感应强度与电流成正比、与该点到导线的距离成反比.一带正电的小球穿在杆上,以初速度v0从a点出发沿杆运动到b点.在a、b、o三点杆对小球的支持力大小分别为Fa、Fb、Fo.下列说法可能正确的是( )| A. | Fa>Fo | B. | Fb>Fa | ||
| C. | 小球一直做匀速直线运动 | D. | 小球先做加速运动后做减速运动 |
| A. | 气体扩散现象表明气体分子间存在斥力 | |
| B. | 将两个分子由极近移动到相距约10倍分子直径的过程中,它们的分子势能先减小后增加 | |
| C. | 热量总是自发地从分子平均动能大的物体传递到分子平均动能减小的物体 | |
| D. | 机械能不可能全部转化为内能,内能也无法全部永爱做功从而转化成机械能 | |
| E. | 液体表面层分子间的距离大于液体内部分子间的距离,所以液体表面分子间的作用表现为相互吸引,即存在表面张力. |
| A. | 加速、减速中的加速度大小之比为a1:a2等于1:1 | |
| B. | 加速、减速中的加速度大小之比为a1:a2等于2:1 | |
| C. | 加速、减速中的位移之比为x1:x2等于2:1 | |
| D. | 加速、减速中的位移之比为x1:x2等于1:2 |
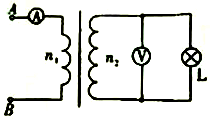 如图所示,理想变化器原副线圈的匝数比n1:n2=1:4,在AB端输入交流电压UAB=15$\sqrt{2}$sin100πt(v),电流表的示数为1A,电路中电流表和电压表均为理想电表,则( )
如图所示,理想变化器原副线圈的匝数比n1:n2=1:4,在AB端输入交流电压UAB=15$\sqrt{2}$sin100πt(v),电流表的示数为1A,电路中电流表和电压表均为理想电表,则( )| A. | 交流电的频率为100Hz | B. | 电压表的示数为60$\sqrt{2}$v | ||
| C. | 灯泡L消耗的功率为15W | D. | 灯泡L的电阻为15Ω |
| A. | 科学史上最伟大的定律之一--万有引力定律是牛顿所发现 | |
| B. | 科学史上,是牛顿第一次提出了“日心说” | |
| C. | 牛顿发现了所有行星围绕太阳运动的轨道都是椭圆 | |
| D. | 牛顿预言了所有行星的轨道的半长轴跟它的公转周期的比值都相等 |

 一棱镜的截面为直角三角形ABC,∠A=30°,直角边BC=a,棱镜材料的折射率为n=$\sqrt{2}$,在此截面所在的平面内,一条光线以45°的入射角从直角边AC的中点M射入棱镜,不考虑光线沿原路返回的情况.求:
一棱镜的截面为直角三角形ABC,∠A=30°,直角边BC=a,棱镜材料的折射率为n=$\sqrt{2}$,在此截面所在的平面内,一条光线以45°的入射角从直角边AC的中点M射入棱镜,不考虑光线沿原路返回的情况.求: