题目内容
(12分)如图所示,在水平轨道右侧安放半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l.水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态.小物块A(可视为质点)从轨道右侧以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧并被弹簧以原速率弹回,经水平轨道返回圆形轨道.
已知R=0.2m,l=1.0m,v0=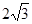 m/s,物块A质量为m=1kg,与PQ段间的动摩擦因数为μ=0.2,轨道其他部分摩擦不计,取g=10m/s2.求:
m/s,物块A质量为m=1kg,与PQ段间的动摩擦因数为μ=0.2,轨道其他部分摩擦不计,取g=10m/s2.求:
(1)物块A与弹簧刚接触时的速度大小.
(2)物块A被弹簧以原速率弹回返回到圆形轨道的高度.
(3)调节PQ段的长度l,A仍以v0从轨道右侧冲上轨道,当l满足什么条件时,A物块能第一次返回圆形轨道且能沿轨道运动而不会脱离轨道.
(1)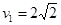 m/s(1分);(2)返回到右边轨道的高度为
m/s(1分);(2)返回到右边轨道的高度为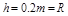 。(1分)
。(1分)
(3)要使A物块能第一次返回圆形轨道并沿轨道运动而不脱离轨道,l满足的条件是 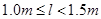 或
或 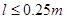 (1分)。
(1分)。
解析试题分析:(1)物块A冲上圆形轨道后回到最低点速度为v0=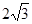 m/s;
m/s;
应用动能定理,与弹簧接触瞬间,有 (1分);
(1分);
可得,物块A与弹簧刚接触时的速度大小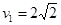 m/s(1分)。
m/s(1分)。
(2)A被弹簧以原速率 弹回,向右经过PQ段,根据匀变速直线运动的规律有
弹回,向右经过PQ段,根据匀变速直线运动的规律有 (1分)
(1分)
得A速度 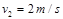 (1分)
(1分)
当A滑上圆形轨道,根据机械能守恒定律有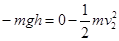 (1分)
(1分)
(也可以应用  )
)
可得,返回到右边轨道的高度为 ,符合实际。(1分)
,符合实际。(1分)
(3)物块A以v0冲上轨道直到回到PQ段右侧,有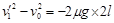
可得,A回到右侧速度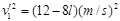 (1分)
(1分)
要使A能返回右侧轨道且能沿轨道运动而不脱离轨道,则有:
①若A沿轨道上滑至最大高度h时,速度减为0,则h满足: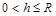 (1分)
(1分)
根据机械能守恒: 联立可得,
联立可得,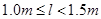 (1分)
(1分)
②若A能沿轨道上滑至最高点,则满足: 且
且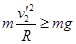 (1分)
(1分)
联立得 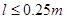 (1分)
(1分)
综上所述,要使A物块能第一次返回圆形轨道并沿轨道运动而不脱离轨道,l满足的条件是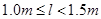 或
或 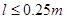 (1分)
(1分)
考点:匀变速直线运动的规律、动能定理及机械能守恒定律的综合应用。

| A、研究地球的自转 | B、研究一列火车的进站时间 | C、研究一列火车从昆明开往丽江的运行时间 | D、研究直升飞机上螺旋桨的转动情况 |
| A、时间和时刻的区别在于长短不同,长的是时间,短的是时刻 | B、两个时刻之间的间隔是一段时间 | C、第三秒末和第四秒初是同一时刻 | D、第三秒内和第六秒内经历的时间一样长 |
A、由公式v=
| ||
| B、物体运动的时间越短,其速度越大 | ||
| C、速度是表示物体运动快慢的物理量 | ||
| D、做匀速直线运动的物体,其位移与时间的比值是一恒量 |
静电力恒量k的单位是
| A.N·m2/kg2 | B.kg2/(N·m2) |
| C.N·m2/C2 | D.C2/(N·m2) |
下列技术应用中,不是利用电磁波工作的是
| A.利用微波雷达跟踪飞行目标 |
| B.利用声呐系统探测海底深度 |
| C.利用北斗导航系统进行定位和导航 |
| D.利用移动通信屏蔽器屏蔽手机信号 |


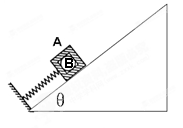
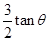 ,槽内紧靠右挡板处有一小物块B,它与凹槽左挡板的距离为d.A、B的质量均为m,斜面足够长.现同时由静止释放A、B,此后B与A挡板每次发生碰撞均交换速度,碰撞时间都极短.已知重力加速度为g.求:
,槽内紧靠右挡板处有一小物块B,它与凹槽左挡板的距离为d.A、B的质量均为m,斜面足够长.现同时由静止释放A、B,此后B与A挡板每次发生碰撞均交换速度,碰撞时间都极短.已知重力加速度为g.求: