题目内容
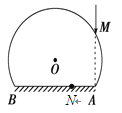
【题目】如图所示,球半径为R的玻璃球冠的底面镀银,底面的半径为![]() R,在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点,经M点折射后的光线照射到底面的N点上,且BN=MN,已知光在真空中的传播速度为c. 求:
R,在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点,经M点折射后的光线照射到底面的N点上,且BN=MN,已知光在真空中的传播速度为c. 求:
①玻璃球冠的折射率;
②该光线在玻璃球冠的传播时间(不考虑光在玻璃球冠中的多次反射)。
【答案】①![]() ②
②![]()
【解析】
(1)光路图如图所示:

由几何关系得![]() ,
,![]() ,OAM为等边三角形,即BOM为一条直线,所以在M点入射角i=600。又BN=MN,所以在M点折射角r=300.
,OAM为等边三角形,即BOM为一条直线,所以在M点入射角i=600。又BN=MN,所以在M点折射角r=300.
由折射定律得![]()
解得![]()
(2)由几何关系可得,在N点反射后的光线过O点垂直BM从球冠的Q点射出
改光线在球冠中的路径![]()
又n=c/v
传播时间t=s/v.
解得![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目