题目内容
15. 两物体M、m用跨过光滑定滑轮的轻绳相连,如图所示,OA、OB与水平面的夹角分别为30°、60°,M、m均处于静止状态.则( )
两物体M、m用跨过光滑定滑轮的轻绳相连,如图所示,OA、OB与水平面的夹角分别为30°、60°,M、m均处于静止状态.则( )| A. | 绳OA的拉力大于绳OB的拉力 | |
| B. | 绳OB的拉力大于绳OA的拉力 | |
| C. | m受到水平面的静摩擦力的方向水平向右 | |
| D. | m受到水平面的静摩擦力的方向水平向左 |
分析 对结点O受力分析,再沿水平方向对正交分解,然后利用平衡条件求出AO、BO绳的张力F1和F2.对m受力分析,两绳对m的拉力为水平向左的F1,水平向右的F2,有平衡条件知F1和F2的差就等于m受到的摩擦力的大小.
解答  解:A、B、对接点O受力分析如图:
解:A、B、对接点O受力分析如图:
把F1和F2分别分解到水平方向和竖直方向.
沿水平方向列方程:
F1cos30°=F2cos60°…①
沿竖直方向列方程:
F1sin30°+F2sin60°=Mg…②
由①②联立得:F1=$\frac{1}{2}$Mg.
F2=$\frac{\sqrt{3}}{2}$Mg,故F2>F1
故A错误,B正确; C、D、对m受力分析如下图:
C、D、对m受力分析如下图:
水平方向列平衡方程:F1+f=F2…③
由③解得:f=F2-F1=$\frac{\sqrt{3}-1}{2}$Mg,故m受到的摩擦力为静摩擦力方向水平向左.故D正确,C错误.
故选:BD.
点评 本题综合了受力分析、正交分解、平衡条件应用等内容.解题过程中要注意研究对象选取,正确选取研究对象是解决此类问题的关键,该题难度中等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.有经验的战士可以从炮弹飞行时的尖叫声判断炮弹的飞行方向,他所利用的是( )
| A. | 声波的干涉现象 | B. | 声波的衍射现象 | ||
| C. | 声波的多普勒效应 | D. | 声波的反射现象 |
3.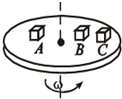 如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )
如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )
 如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )
如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )| A. | 每个物体均受重力、支持力、静摩擦力、向心力四个力作用 | |
| B. | A的向心加速度大于B的向心加速度 | |
| C. | B和C所受摩擦力相等 | |
| D. | 若逐渐增大圆盘转速,C比B先滑动,A和B同时滑动 |
20.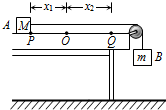 为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.
为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.
(1)请根据如表的实验数据在答题纸上的坐标图中作出x1-x2关系图象.
(2)木块与桌面之间的动摩擦因数μ=$\frac{{m{x_1}}}{{(M+m){x_2}+M{x_1}}}$(用M、m、x1、x2表示).
(3)实验中,细线与滑轮之间的摩擦以及滑轮轴的摩擦会导致的测量结果偏大(选填“偏大”、“偏小”或“无影响”).
 为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.
为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.(1)请根据如表的实验数据在答题纸上的坐标图中作出x1-x2关系图象.
| x1(cm) | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 |
| x2(cm) | 19.5 | 28.5 | 39.0 | 48.0 | 56.5 |
(3)实验中,细线与滑轮之间的摩擦以及滑轮轴的摩擦会导致的测量结果偏大(选填“偏大”、“偏小”或“无影响”).
7.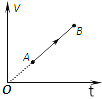 一定质量的理想气体V-t的图象如图所示,在气体由状态A变化到状态B的过程中,气体的压强( )
一定质量的理想气体V-t的图象如图所示,在气体由状态A变化到状态B的过程中,气体的压强( )
 一定质量的理想气体V-t的图象如图所示,在气体由状态A变化到状态B的过程中,气体的压强( )
一定质量的理想气体V-t的图象如图所示,在气体由状态A变化到状态B的过程中,气体的压强( )| A. | 一定不变 | B. | 一定减小 | ||
| C. | 一定增大 | D. | 不能判断怎样变化 |
 如图所示,已知某人骑自行车每分钟蹬30圈,车轮与脚蹬轮盘转数之比为4:1,车轮半径为0.50m,则求车轮转动的线速度为6.28m/s.
如图所示,已知某人骑自行车每分钟蹬30圈,车轮与脚蹬轮盘转数之比为4:1,车轮半径为0.50m,则求车轮转动的线速度为6.28m/s. 如图所示,有两个相邻的有界匀强磁场区域,磁感应强度的大小均为B,磁场方向相反,且与纸面垂直,磁场区域在x轴方向宽度均为a,在y轴方向足够宽.现有一高为a的正三角形导线框从图示位置开始向右匀速穿过磁场区域.若以逆时针方向为电流的正方向,在下图中,线框中感应电流i与线框移动距离x的关系图象正确的是( )
如图所示,有两个相邻的有界匀强磁场区域,磁感应强度的大小均为B,磁场方向相反,且与纸面垂直,磁场区域在x轴方向宽度均为a,在y轴方向足够宽.现有一高为a的正三角形导线框从图示位置开始向右匀速穿过磁场区域.若以逆时针方向为电流的正方向,在下图中,线框中感应电流i与线框移动距离x的关系图象正确的是( )

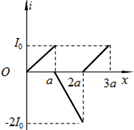
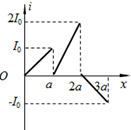
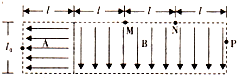 如图所示,纸面内有边长为l的正方形区域A和宽度为l,长为3l的长方形区域B,区域A内存在着水平向左、场强大小为E0的匀强电场,区域A左边界中点O处可不断供给初速度为零,带电量为q,质量为m的带负电的粒子,单位时间供给粒子数量为n,区域B内存在一个方向向下,场强大小与时间成正比的匀强电场(E=kt,当有粒子刚进入区域B时开始计时),不计重力,空气阻力及粒子间的相互作用,由于粒子的速度很大,运动时间极短,粒子从进入区域B到最终离开区域B的过程中电场强度可认为不变
如图所示,纸面内有边长为l的正方形区域A和宽度为l,长为3l的长方形区域B,区域A内存在着水平向左、场强大小为E0的匀强电场,区域A左边界中点O处可不断供给初速度为零,带电量为q,质量为m的带负电的粒子,单位时间供给粒子数量为n,区域B内存在一个方向向下,场强大小与时间成正比的匀强电场(E=kt,当有粒子刚进入区域B时开始计时),不计重力,空气阻力及粒子间的相互作用,由于粒子的速度很大,运动时间极短,粒子从进入区域B到最终离开区域B的过程中电场强度可认为不变