题目内容
8.宇宙中两颗相距很近的恒星常常组成一个双星系统.它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动.若已知它们的运动周期为T,两星到某一共同圆心的距离分别为R1和R2.那么,双星系统中两颗恒星的质量关系是( )| A. | 必有一颗恒星的质量为$\frac{{4{π^2}{R_1}{{({R_1}+{R_2})}^2}}}{{G{T^2}}}$ | |
| B. | 这两颗恒星的质量之和为$\frac{{4{π^2}{{({R_1}+{R_2})}^3}}}{{G{T^2}}}$ | |
| C. | 这两颗恒星的质量之比为m1:m2=R2:R1 | |
| D. | 这两颗恒星的质量必定相等 |
分析 由双星系统两个星体受的万有引力相等,故有此可以求得各自的质量表达式,以及质量之比
解答 解:A、D、对m1有:$G\frac{{m}_{1}{m}_{2}}{({R}_{1}+{R}_{2})^{2}}$=${m}_{1}{R}_{1}\frac{4{π}^{2}}{{T}^{2}}$,解得:m2=$4{π}^{2}\frac{{R}_{1}({R}_{1}+{R}_{2})^{2}}{G{T}^{2}}$,同理可得:${m}_{1}=\frac{4{π}^{2}{R}_{2}({R}_{1}+{R}_{2})^{2}}{G{T}^{2}}$,故A正确,D错误
B:由A两者质量相加得:$\frac{{4{π^2}{{({R_1}+{R_2})}^3}}}{{G{T^2}}}$则B正确
C:由A知m1:m2=R2:R1故C正确.
故选:ABC
点评 本题主要是依据双星的两个共同量:引力和周期,来列相应的表达式,进而才能解得需要的结果.这两个共同量一般是解决双星问题的关键

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
15.关于磁感线,下列说法正确的是( )
| A. | 磁感线在磁场中并不真实存在,而是为了形象地描述磁场人为引入的一簇曲线 | |
| B. | 磁感线密集的地方磁场强 | |
| C. | 磁感线稀疏的地方磁场强 | |
| D. | 磁感线上某点的切线方向为该点的磁场方向 |
3.某物理兴趣小组先用伏安法来测定一干电池的电动势和内电阻.现有以下器材可供选用:
A.电流计G1(量程3.0mA,内阻Rg=10Ω)
B.电流计G2(量程5.0mA,内阻约为1Ω)
C.电流表A(量程0.6A,内阻约为0.50Ω)
D.滑动变阻器R1(0~20Ω,10A)
E.电阻箱R2
F.开关S和导线若干
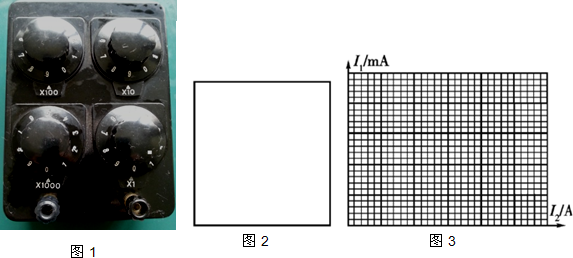
(1)实验小组先用电流计和电阻箱通过改装成一个电压表,则电流计应选用G1.(填G1或G2).所用的电阻箱阻值如图1所示,读数是990Ω.
(2)请在图2线框内画出该实验小组所采用的实验电路图.(标注所选择的器材符号)
(3)该小组在(1)、(2)的基础上根据实验设计的电路图测得的数据如表,请你在图3坐标纸上选择合理的标度,并作出相应的图线.
(4)根据(3)中的图线求得电源的电动势E=1.48V(保留三位有效数字),电源的内阻r=0.84Ω(保留两位有效数字)
A.电流计G1(量程3.0mA,内阻Rg=10Ω)
B.电流计G2(量程5.0mA,内阻约为1Ω)
C.电流表A(量程0.6A,内阻约为0.50Ω)
D.滑动变阻器R1(0~20Ω,10A)
E.电阻箱R2
F.开关S和导线若干

(1)实验小组先用电流计和电阻箱通过改装成一个电压表,则电流计应选用G1.(填G1或G2).所用的电阻箱阻值如图1所示,读数是990Ω.
(2)请在图2线框内画出该实验小组所采用的实验电路图.(标注所选择的器材符号)
(3)该小组在(1)、(2)的基础上根据实验设计的电路图测得的数据如表,请你在图3坐标纸上选择合理的标度,并作出相应的图线.
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 电流表G(I1/mA) | 1.36 | 1.34 | 1.26 | 1.24 | 1.18 | 1.12 |
| 电流表A(I2/A) | 0.12 | 0.16 | 0.20 | 0.28 | 0.36 | 0.44 |
13. 如图所示,分别沿倾角不同的斜面由静止向上拉同一个物体,物体与各斜面间动摩擦因数相同,拉力方向与各斜面均保持平行,物体沿不同斜面作匀加速直线运动的加速度大小均相同,上升的竖直高度也相同.在此过程中( )
如图所示,分别沿倾角不同的斜面由静止向上拉同一个物体,物体与各斜面间动摩擦因数相同,拉力方向与各斜面均保持平行,物体沿不同斜面作匀加速直线运动的加速度大小均相同,上升的竖直高度也相同.在此过程中( )
 如图所示,分别沿倾角不同的斜面由静止向上拉同一个物体,物体与各斜面间动摩擦因数相同,拉力方向与各斜面均保持平行,物体沿不同斜面作匀加速直线运动的加速度大小均相同,上升的竖直高度也相同.在此过程中( )
如图所示,分别沿倾角不同的斜面由静止向上拉同一个物体,物体与各斜面间动摩擦因数相同,拉力方向与各斜面均保持平行,物体沿不同斜面作匀加速直线运动的加速度大小均相同,上升的竖直高度也相同.在此过程中( )| A. | 无论沿什么斜面拉,克服摩擦力做的功相同 | |
| B. | 无论沿什么斜面拉,合外力做的功均相同 | |
| C. | 沿倾角较大的斜面拉,克服重力做的功较多 | |
| D. | 沿倾角较小的斜面拉,合外力做的功较多 |
20.布朗运动是说明分子运动的重要实验事实,关于布朗运动,下列说法中正确的是( )
| A. | 布朗运动是液体分子的无规则运动 | |
| B. | 布朗运动是悬浮在液体中的固体分子的无规则运动 | |
| C. | 布朗运动产生的原因是液体分子对小颗粒碰撞时产生的作用力不平衡引起的 | |
| D. | 悬浮的小颗粒越大,撞击它的分子数越多,布朗运动越剧烈 |
 投石机是上古时代的一种攻城武器,它可把巨石投进敌方的城墙和城内,造成破坏,图示为一投石机装置,投石机把质量为m的巨石先从地面升到离地h的高度再抛射出去,假设巨石被抛射除去后所做的运动是平抛运动,其落点离抛出点的水平距离为x,不计空气阻力,重力加速度为g,求:
投石机是上古时代的一种攻城武器,它可把巨石投进敌方的城墙和城内,造成破坏,图示为一投石机装置,投石机把质量为m的巨石先从地面升到离地h的高度再抛射出去,假设巨石被抛射除去后所做的运动是平抛运动,其落点离抛出点的水平距离为x,不计空气阻力,重力加速度为g,求: 某同学在实验室做“用油膜法估测分子直径大小”的实验中,实验的方法及步骤如下:
某同学在实验室做“用油膜法估测分子直径大小”的实验中,实验的方法及步骤如下: 如图所示,一个质量m=5kg的物体放在光滑水平面上.对物体施加一个F=5N的水平拉力,使物体由静止开始做匀加速直线运动,经过时间t=4s,求:
如图所示,一个质量m=5kg的物体放在光滑水平面上.对物体施加一个F=5N的水平拉力,使物体由静止开始做匀加速直线运动,经过时间t=4s,求: