��Ŀ����
13�� Ͷʯ�����Ϲ�ʱ����һ�ֹ������������ɰѾ�ʯͶ���з��ij�ǽ�ͳ��ڣ�����ƻ���ͼʾΪһͶʯ��װ�ã�Ͷʯ��������Ϊm�ľ�ʯ�ȴӵ����������h�ĸ߶��������ȥ�������ʯ�������ȥ���������˶���ƽ���˶�����������׳����ˮƽ����Ϊx�����ƿ����������������ٶ�Ϊg����
Ͷʯ�����Ϲ�ʱ����һ�ֹ������������ɰѾ�ʯͶ���з��ij�ǽ�ͳ��ڣ�����ƻ���ͼʾΪһͶʯ��װ�ã�Ͷʯ��������Ϊm�ľ�ʯ�ȴӵ����������h�ĸ߶��������ȥ�������ʯ�������ȥ���������˶���ƽ���˶�����������׳����ˮƽ����Ϊx�����ƿ����������������ٶ�Ϊg������1����ʯ����ߵ���ٶȴ�С��
��2��Ͷʯ���Ѿ�ʯ�ӵ������ߣ��������ȥ�Ĺ����У��Ծ�ʯ���Ĺ���
���� ��1����ʯ��ƽ���˶������˶��ֽ⼴�������ʯ����ߵ���ٶȣ�
��2��Ͷʯ���Ѿ�ʯ�ӵ������ߣ��������ȥ�Ĺ����У��Ծ�ʯ���Ĺ�ת��Ϊ��ʯ�Ķ��ܺ��������ܣ����ݹ��ܹ�ϵ���������
��� �⣺��1����ʯ��ƽ���˶�����ֱ����h=$\frac{1}{2}g{t}^{2}$
�����˶���ʱ�䣺t=$\sqrt{\frac{2h}{g}}$
ˮƽ����x=vt
���ԣ�v=$\frac{x}{t}=x•\sqrt{\frac{g}{2h}}$
��2��Ͷʯ���Ѿ�ʯ�ӵ������ߣ��������ȥ�Ĺ����У��Ծ�ʯ���Ĺ�ת��Ϊ��ʯ�Ķ��ܺ��������ܣ����ݹ��ܹ�ϵ�ã�
W=mgh+$\frac{1}{2}m{v}^{2}$=$mg��h+\frac{{x}^{2}}{4h}��$
�𣺣�1����ʯ����ߵ���ٶȴ�С��$x•\sqrt{\frac{g}{2h}}$��
��2��Ͷʯ���Ѿ�ʯ�ӵ������ߣ��������ȥ�Ĺ����У��Ծ�ʯ���Ĺ���$mg��h+\frac{{x}^{2}}{4h}��$��
���� ��������ʯ��Ϊģ�ͣ�����ƽ���˶��빦�ܹ�ϵ��������������Զ����ģ��ֱ�ʹ����Ӧ�Ĺ�ʽ���ɣ�������Ŀ��

��ϰ��ϵ�д�
 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
�����Ŀ
3���ִ����е�·���Ե�·���Dz����Զ����Ƶģ�����Ȼ������ȵ���ij��ֵʱ·�����Զ�����������Ȼ������ȸ���ij��ֵʱ��·�����Զ�Ϩ������Ϊ��·���Զ����Ƶ�·�в������������ִ�������������
| A�� | �¶ȴ����� | B�� | ѹ�������� | C�� | ����� | D�� | ���������� |
4�� �������ⶨ�����������ʵ�ʵ��ʱ������������治��ֱ��������ͼ��a����ʾ����б�����ڷ��ò���שʱ������ש��ƽ��û����aa���غϣ�������ͼ��b����ʾ��ƫ������Dz�õ������ʱ���ʵֵ��������
�������ⶨ�����������ʵ�ʵ��ʱ������������治��ֱ��������ͼ��a����ʾ����б�����ڷ��ò���שʱ������ש��ƽ��û����aa���غϣ�������ͼ��b����ʾ��ƫ������Dz�õ������ʱ���ʵֵ��������
 �������ⶨ�����������ʵ�ʵ��ʱ������������治��ֱ��������ͼ��a����ʾ����б�����ڷ��ò���שʱ������ש��ƽ��û����aa���غϣ�������ͼ��b����ʾ��ƫ������Dz�õ������ʱ���ʵֵ��������
�������ⶨ�����������ʵ�ʵ��ʱ������������治��ֱ��������ͼ��a����ʾ����б�����ڷ��ò���שʱ������ש��ƽ��û����aa���غϣ�������ͼ��b����ʾ��ƫ������Dz�õ������ʱ���ʵֵ��������| A�� | ��ƫС | B�� | �ҵ�ƫС | C�� | ��ƫ�� | D�� | �ҵ�ƫ�� |
1�����κ���ȵ�����ʱ���������ٶȵı仯����ͬ���˶��ǣ�������
| A�� | ���������˶� | B�� | ƽ���˶� | C�� | �ȼ���ֱ���˶� | D�� | ����Բ���˶� |
8��һ����Ϊm�������ھ���ˮƽ����ĸ߶�Ϊh���Գ��ٶ�v0��ƽ���˶�������$\frac{h}{2}$�߶�ʱ�����Ĺ����ǣ�������
| A�� | $\frac{1}{2}$mgv0 | B�� | mg$\sqrt{gh}$ | C�� | mg$\sqrt{2gh}$ | D�� | mgv0 |
8���������������ܽ��ĺ��dz������һ��˫��ϵͳ���������������������˴��ṩ���������Ӷ�ʹ��������ijһ��ͬ��Բ��������Բ���˶�������֪���ǵ��˶�����ΪT�����ǵ�ijһ��ͬԲ�ĵľ���ֱ�ΪR1��R2����ô��˫��ϵͳ�����ź��ǵ�������ϵ�ǣ�������
| A�� | ����һ�ź��ǵ�����Ϊ$\frac{{4{��^2}{R_1}{{��{R_1}+{R_2}��}^2}}}{{G{T^2}}}$ | |
| B�� | �����ź��ǵ�����֮��Ϊ$\frac{{4{��^2}{{��{R_1}+{R_2}��}^3}}}{{G{T^2}}}$ | |
| C�� | �����ź��ǵ�����֮��Ϊm1��m2=R2��R1 | |
| D�� | �����ź��ǵ������ض���� |
5����ͼ�����������ڲ�ͬ�¶ȣ�0���100�棩�µ����ʷֲ�����ͼ��֪��Ϣ��������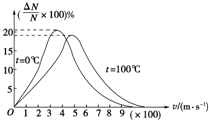

| A�� | ͬһ�¶��£��������ӵ����ʷֲ����ֳ����м�࣬��ͷ�١��ķֲ����� | |
| B�� | �����¶ȵ����ߣ�ÿһ���������ӵ����ʶ����� | |
| C�� | �����¶ȵ����ߣ���������������С�ķ�����ռ�ı������� | |
| D�� | �����¶ȵ����ߣ��������ӵ�ƽ�����ʱ�С |
 �ҹ��ĺ��캽����ҵȡ���˾�ijɾͣ�2013��12��14�ţ����϶����š�̽�����������ϵĺ������ɹ�ʵ������½�����϶����š�����½ǰ�����˷�����졢����ת�ơ����·��е�һϵ�й��̣���ͼΪ���϶����š��ķ��й��ʾ��ͼ����֪���������������ٶ�Ϊg��������뾶ΪR������������ת��Ӱ�죮
�ҹ��ĺ��캽����ҵȡ���˾�ijɾͣ�2013��12��14�ţ����϶����š�̽�����������ϵĺ������ɹ�ʵ������½�����϶����š�����½ǰ�����˷�����졢����ת�ơ����·��е�һϵ�й��̣���ͼΪ���϶����š��ķ��й��ʾ��ͼ����֪���������������ٶ�Ϊg��������뾶ΪR������������ת��Ӱ�죮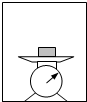 С����ͬѧһ����̨���ڵ�����̽��������ʧ��������ͼ��ʾ��̨������ˮƽ��������Ϊ10N��������������ϣ������ݾ�ֹ����̨�ӵ�ʾ��Ϊ10N����̨�ӵ�ʾ��Ϊ8N������ݵ��˶������Ǽ����½������������ѡ��������������������½��������������������������½�����
С����ͬѧһ����̨���ڵ�����̽��������ʧ��������ͼ��ʾ��̨������ˮƽ��������Ϊ10N��������������ϣ������ݾ�ֹ����̨�ӵ�ʾ��Ϊ10N����̨�ӵ�ʾ��Ϊ8N������ݵ��˶������Ǽ����½������������ѡ��������������������½��������������������������½�����