题目内容
空间探测器从某一星球表面竖直升空,已知探测器质量为500 kg（设为恒量）,发动机推力为恒力,探测器升空后发动机因故障而突然关闭,如图4-6-10所示是探测器从升空到落回星球表面的速度—时间图象,则由图象可判断该探测器在星球表面所能达到的最大高度是多少?发动机工作时的推力是多大?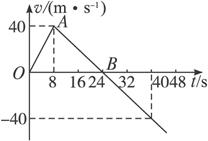
图4-6-10
思路解析：本题是根据图象来表达有关已知条件的.正确理解v-t图象各段斜率、各转折点、各块面积的含义是解答本题的关键.
由图可知,空间探测器在t1=8 s时具有最大即时速度,t2=24 s时才达到最大高度,且其最大高度为图象中△OAB的面积,即hmax=
×24×40 m=480 m.
空间探测器在8 s内在推动力和重力作用下加速上升,在8 s后只在重力作用下减速上升和加速回落.
第一阶段加速度a1=
m/s2=5 m/s2
第二、三阶段加速度相等，为a2=
m/s2=-2.5 m/s2
据牛顿第二定律,第一阶段F-mg星=ma1 ①
第二、三阶段-mg星=ma2 ②
由①②得：F=m（a1-a2）=500×7.5 N=3 750 N.
答案：480 m 3 750 N
练习册系列答案
相关题目
空间探测器从某一星球表面竖直升空，已知探测器质量为500kg（设为恒量），发动机推力为恒力，探测器升空后发动机因故障而突然关闭，如图所示为探测器从升空到落回星球表面的速度-时间图象，则由图象可判断该探测器在星球表面所能达到的最大高度是多少？发动机工作时的推力又为多大？
空间探测器从某一星球表面竖直升空，发动机推力为恒力．探测器升空后发动机因故障突然关闭，探测器升空到落回星球表面的速度随时间变化的图象如图所示，根据图象，求：
空间探测器从某一星球表面（星球表面真空）竖直升空，已知探测器质量为1500kg（设为恒量），发动机推动力为恒力．探测器升空后发动机因故障突然关闭，如图是探测器从升空到落回星球表面的速度随时间变化的图线，则由图象及计算求：
一空间探测器从某一星球表面竖直升空，假设探测器质量恒为1500kg，发动机推动力F为恒力，若探测器升空过程中发动机突然关闭，其速度随时间的变化情况如图所示，图线上A、B、C三点对应的时刻分别为9s、25s和45s．已知该星球表面没有空气．试求：
空间探测器从某一星球表面竖直升空，已知探测器质量为500kg（设为恒量），发动机竖直推力为恒力，探测器升空后发动机因故障而突然关闭，同时自动修复程序启动，短时间内修复成功，恰好使探测器安全返回星球表面．如图所示是探测器的速度--时间图象，由图象可判断该探测器（ ）