题目内容
17.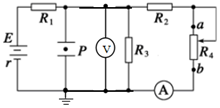 如图所示电路,平行金属板中带负电的小球被固定在P处,不计电流表和电压表内阻对电路的影响,选地面的电势为零.当滑动变阻器R4的滑片向b端移动时,下列说法正确的是( )
如图所示电路,平行金属板中带负电的小球被固定在P处,不计电流表和电压表内阻对电路的影响,选地面的电势为零.当滑动变阻器R4的滑片向b端移动时,下列说法正确的是( )| A. | 电压表读数减小 | |
| B. | 小球的电势能减小 | |
| C. | 电源的效率增大 | |
| D. | 若电压表、电流表的示数变化量分别为△U和△I,则$\frac{|△U|}{|△I|}$<r+R1 |
分析 先由滑片的移动方向判断电路中电阻的变化,再由闭合电路欧姆定律可知各电表示数的变化及电容器两端的电压变化;再分析P点的电势变化情况,从而分析出小球的电势能如何变化.根据内外电阻的关系分析电源的效率如何变化.根据闭合电路欧姆定律分析$\frac{|△U|}{|△I|}$.
解答 解:A、当R4的滑片向b移动时,滑动变阻器接入电路的有效电阻减小,则电路中总电阻减小;由闭合电路欧姆定律可知,电路中总电流增大;路端电压减小,同时R1两端的电压也增大,故并联部分的电压减小,电压表读数减小,故A正确.
B、并联部分的电压减小,电容器两板间的电压减小,板间场强减小,由U=Ed知,P点与电容器下极板间的电势差减小,而P点的电势高于零电势,所以P点的电势减小,由于小球带负电,所以小球的电势能增大,故B错误;
C、由于电源的内外电阻关系未知,所以不能确定电源的效率如何变化,故C错误.
D、设电路中总电流为I总.根据闭合电路欧姆定律有 U=E-I总(r+R1),则|$\frac{△U}{△{I}_{总}}$|=r+R1.
根据总电流增大,流过R3的电流减小,则知电流表示数增大,且有|△I|>|△I总|,则$\frac{|△U|}{|△I|}$<|$\frac{△U}{△{I}_{总}}$|=r+R1.故D正确.
故选:AD
点评 解决闭合电路欧姆定律的题目,一般可以按照整体-局部-整体的思路进行分析,要注意电路中某一部分电阻减小时,无论电路的连接方式如何,总电阻均是减小的.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
13.关于地球同步卫星的下述说法中,正确的是( )
| A. | 同步卫星要和地球自转同步,它离地面的高度和环行速率都是确定的 | |
| B. | 同步卫星的角速度和地球自转角速度相同.但同步卫星的高度和环行速率可以选择 | |
| C. | 我国发射的同步卫星可以定点在北京上空 | |
| D. | 同步卫星的轨道可以不在地球赤道平面内 |
8.关于线圈在匀强磁场中转动产生的交流电,以下说法中正确的是( )
| A. | 线圈每转动一周,感应电流方向就改变一次 | |
| B. | 线圈平面每经过中性面一次,感应电流方向就改变一次,感应电动势方向不变 | |
| C. | 线圈在中性面位置时,磁通量最大,磁通量的变化率为零 | |
| D. | 线圈在与中性面垂直的位置时,磁通量为零,感应电动势最大 |
5.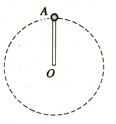 如图所示,小球A质量为m,固定在长为L的轻细直杆一端,绕杆的另一端O点在竖直平面内做圆周运动.若小球经过最低点时的速度为$\sqrt{6gL}$,不计一切阻力,则小球运动到最高点时,杆对球的作用力为( )
如图所示,小球A质量为m,固定在长为L的轻细直杆一端,绕杆的另一端O点在竖直平面内做圆周运动.若小球经过最低点时的速度为$\sqrt{6gL}$,不计一切阻力,则小球运动到最高点时,杆对球的作用力为( )
 如图所示,小球A质量为m,固定在长为L的轻细直杆一端,绕杆的另一端O点在竖直平面内做圆周运动.若小球经过最低点时的速度为$\sqrt{6gL}$,不计一切阻力,则小球运动到最高点时,杆对球的作用力为( )
如图所示,小球A质量为m,固定在长为L的轻细直杆一端,绕杆的另一端O点在竖直平面内做圆周运动.若小球经过最低点时的速度为$\sqrt{6gL}$,不计一切阻力,则小球运动到最高点时,杆对球的作用力为( )| A. | 推力,大小为mg | B. | 拉力,大小为mg | ||
| C. | 拉力,大小为0.5mg | D. | 推力,大小为0.5mg |
2.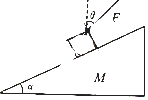 一倾角为α的斜劈M放在水平面上,一物体m沿斜劈匀速下滑,现在给物体施加如图所示的力F,F与竖直方向的夹角为θ,斜劈仍静止,则以下说法正确的是( )
一倾角为α的斜劈M放在水平面上,一物体m沿斜劈匀速下滑,现在给物体施加如图所示的力F,F与竖直方向的夹角为θ,斜劈仍静止,则以下说法正确的是( )
 一倾角为α的斜劈M放在水平面上,一物体m沿斜劈匀速下滑,现在给物体施加如图所示的力F,F与竖直方向的夹角为θ,斜劈仍静止,则以下说法正确的是( )
一倾角为α的斜劈M放在水平面上,一物体m沿斜劈匀速下滑,现在给物体施加如图所示的力F,F与竖直方向的夹角为θ,斜劈仍静止,则以下说法正确的是( )| A. | 斜劈M对地的摩擦力为0 | |
| B. | 斜劈M对地的摩擦力方向向左 | |
| C. | 斜劈M对地的摩擦力方向向右 | |
| D. | 若F与竖直方向的夹角θ=0°,则m将保持匀速运动,M对地无摩擦力的作用 |
6.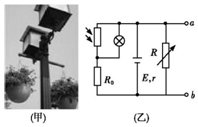 某学校创建绿色校园,如图(甲)为新装的一批节能路灯,该路灯通过光控开关实现自动控制.如图(乙)为其内部控制电路简化原理图,a,b端接路灯电源的开关,要求Uab大于某一值时,接通路灯电路,该控制电路中电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( )
某学校创建绿色校园,如图(甲)为新装的一批节能路灯,该路灯通过光控开关实现自动控制.如图(乙)为其内部控制电路简化原理图,a,b端接路灯电源的开关,要求Uab大于某一值时,接通路灯电路,该控制电路中电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( )
 某学校创建绿色校园,如图(甲)为新装的一批节能路灯,该路灯通过光控开关实现自动控制.如图(乙)为其内部控制电路简化原理图,a,b端接路灯电源的开关,要求Uab大于某一值时,接通路灯电路,该控制电路中电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( )
某学校创建绿色校园,如图(甲)为新装的一批节能路灯,该路灯通过光控开关实现自动控制.如图(乙)为其内部控制电路简化原理图,a,b端接路灯电源的开关,要求Uab大于某一值时,接通路灯电路,该控制电路中电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( )| A. | 电源路端电压不变 | B. | R0两端电压变大 | ||
| C. | 指示灯变暗,Uab变大 | D. | 电源总功率不变 |
7.在一小型交流发电机中,矩形金属线圈abcd的面积为S,匝数为n,线圈总电阻为r,在磁感应强度为B的匀强磁场中,绕轴以角速度ω匀速转动(如图1所示),产生的感应电动势随时间的变化关系(如图2所示),矩形线圈与阻值为R的电阻构成闭合电路,下列说法中正确的是( )
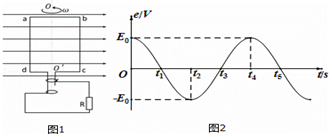

| A. | 从t1到t3这段时间内穿过线圈磁通量的变化量为零 | |
| B. | 从t3到t4这段时间通过电阻R的电荷量为$\frac{{E}_{0}}{(R+r)ω}$ | |
| C. | t4时刻穿过线圈的磁通量的变化率大小为$\frac{{E}_{0}}{n}$ | |
| D. | t4时刻电阻R的发热功率为$\frac{{{E}_{0}}^{2}R}{(R+r)^{2}}$ |
 如图所示,水平面上一个光滑金属框架上垂直放置一根长l=0.4m的金属棒ab,其电阻r=0.1Ω,框架左端的电阻R=0.4Ω.垂直框面的匀强磁场的磁感应强度B=0.1T.当用外力使棒ab以速度v=5m/s右移时,求:
如图所示,水平面上一个光滑金属框架上垂直放置一根长l=0.4m的金属棒ab,其电阻r=0.1Ω,框架左端的电阻R=0.4Ω.垂直框面的匀强磁场的磁感应强度B=0.1T.当用外力使棒ab以速度v=5m/s右移时,求: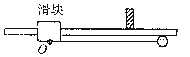 图中滑块质量为m,小球的质量为2m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为1.开始时,轻绳处于水平拉直状态,小球与滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定在导轨上的挡板粘住.在极短的时间内速度减为零.求:
图中滑块质量为m,小球的质量为2m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为1.开始时,轻绳处于水平拉直状态,小球与滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定在导轨上的挡板粘住.在极短的时间内速度减为零.求: